题目内容
【题目】一个等腰三角形的底边长为 5,一腰上中线把其周长分成的两部分的差为 3,则这个等腰三角形的腰长为( )
A.2
B.8
C.2 或 8
D.10
【答案】B
【解析】∵BD为中线,AB=AC,BC=5,
∴AD=CD,
∵C△ABD=AB+BD+AD,C△CBD=BC+CD+BD,
①当C△ABD-C△CBD=3时,
∴AB+BD+AD-(BC+CD+BD)=3,
即AB-BC=3,
∴AB=3+5=8,
∴△ABC三边长分别为:8,8,5,符合三角形三边之间的关系,
②当C△CBD-C△ABD=3时,
∴BC+CD+BD-(AB+BD+AD)=3,
即BC-AB=3,
∴AB=5-3=2,
∴△ABC三边长分别为:2,2,5,2+2![]() 5,不符合三角形三边之间的关系,
5,不符合三角形三边之间的关系,
所以答案是:B.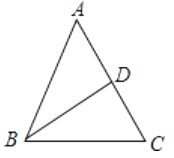
【考点精析】根据题目的已知条件,利用等腰三角形的性质的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目