题目内容
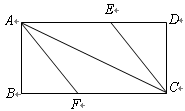
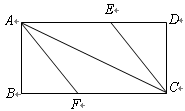
在如图所示的一张矩形纸片ABCD(AD>AB)中,将纸片折叠一次,使点A与C重合,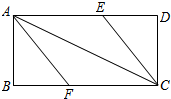 再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.
再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:2AE2=AC•AP;
(3)若AE=8cm,△ABF的面积为9cm2,求△ABF的周长.
分析:(1)连接EF交AC于O,当顶点A与C重合时,折痕EF垂直平分AC,可得OA=OC,∠AOE=∠COF=90°,再利用矩形的性质求证
△AOE≌△COF,即可.
(2)过E作EP⊥AD交AC于P,由作法,∠AEP=90°,求证△AOE∽△AEP,可得
=
,再利用四边形AFCE是菱形,可得AO=
AC,AE2=
AC•AP.即可.
(3)根据四边形AFCE是菱形,可得AF=AE=8.设AB=x,BF=y,可得(x+y)2-2xy=64①再根据三角形面积公式可得xy=18.②然后解方程即可.
△AOE≌△COF,即可.
(2)过E作EP⊥AD交AC于P,由作法,∠AEP=90°,求证△AOE∽△AEP,可得
| AE |
| AP |
| AO |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据四边形AFCE是菱形,可得AF=AE=8.设AB=x,BF=y,可得(x+y)2-2xy=64①再根据三角形面积公式可得xy=18.②然后解方程即可.
解答: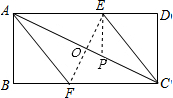 解:(1)连接EF交AC于O,
解:(1)连接EF交AC于O,
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF.
∴OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴平行四边形AFCE是菱形.
(2)证明:过E作EP⊥AD交AC于P,
由作法,∠AEP=90°,
由(1)知:∠AOE=90°,又∠EAO=∠EAP,
∴△AOE∽△AEP,
∴
=
,则AE2=AO•AP,
∵四边形AFCE是菱形,
∴AO=
AC,
∴AE2=
AC•AP.
∴2AE2=AC•AP.
(3)∵四边形AFCE是菱形,
∴AF=AE=8.
设AB=x,BF=y,
∵∠B=90,即三角形ABC为直角三角形,
∴x2+y2=64,
∴(x+y)2-2xy=64①,
又∵S△ABF=9,∴
xy=9,则xy=18②,
由①、②得:(x+y)2=100,
∴x+y=10,x+y=-10(不合题意舍去),
∴△ABF的周长为x+y+AF=10+8=18.
 解:(1)连接EF交AC于O,
解:(1)连接EF交AC于O,当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF.
∴OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴平行四边形AFCE是菱形.
(2)证明:过E作EP⊥AD交AC于P,
由作法,∠AEP=90°,
由(1)知:∠AOE=90°,又∠EAO=∠EAP,
∴△AOE∽△AEP,
∴
| AE |
| AP |
| AO |
| AE |
∵四边形AFCE是菱形,
∴AO=
| 1 |
| 2 |
∴AE2=
| 1 |
| 2 |
∴2AE2=AC•AP.
(3)∵四边形AFCE是菱形,
∴AF=AE=8.
设AB=x,BF=y,
∵∠B=90,即三角形ABC为直角三角形,
∴x2+y2=64,
∴(x+y)2-2xy=64①,
又∵S△ABF=9,∴
| 1 |
| 2 |
由①、②得:(x+y)2=100,
∴x+y=10,x+y=-10(不合题意舍去),
∴△ABF的周长为x+y+AF=10+8=18.
点评:此题主要考查相似三角形的判定与性质,全等三角形的判定与性质,菱形的判定与性质,有一定的拔高难度,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
(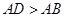 )中,将纸片折叠一次,使点
)中,将纸片折叠一次,使点 与
与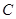 重合,再展开,折痕
重合,再展开,折痕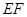 交
交 边于
边于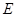 ,交
,交 边于
边于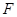 ,分别连结
,分别连结 和
和 .
.
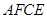 是菱形;
是菱形;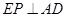 交
交 于
于 ,求证:
,求证:
 ,
, 的面积为
的面积为 ,求
,求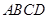 (
(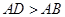 )中,将纸片折叠一次,使点
)中,将纸片折叠一次,使点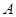 与
与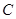 重合,再展开,折痕
重合,再展开,折痕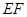 交
交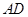 边于
边于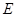 ,交
,交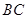 边于
边于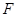 ,分别连结
,分别连结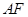 和
和 .
.
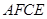 是菱形;
是菱形;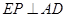 交
交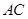 于
于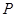 ,求证:
,求证: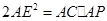
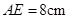 ,
,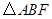 的面积为
的面积为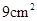 ,求
,求 (
(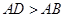 )中,将纸片折叠一次,使点
)中,将纸片折叠一次,使点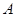 与
与 重合,再展开,折痕
重合,再展开,折痕 交
交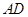 边于
边于 ,交
,交 边于
边于 ,分别连结
,分别连结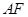 和
和 .
.
 是菱形;
是菱形;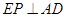 交
交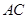 于
于 ,求证:
,求证:
 ,
, 的面积为
的面积为 ,求
,求