题目内容
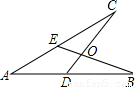
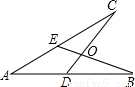
 如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.
如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.
(1)请你写出一个正确的命题,并加以证明;
(2)请你至少写出三个这样的正确命题.
(1)如果AE=AD,AB=AC,那么∠B=∠C.
证明:在△ABE和△ACD中,
∵ ,
,
∴△ABE≌△ACD,
∴∠B=∠C.
(2)解:①如果AE=AD,AB=AC,那么OB=OC.
②如果AE=AD,∠B=∠C,那么AB=AC.
③如果OB=OC,∠B=∠C,那么AE=AD.
分析:(1)如果AE=AD,AB=AC,那么∠B=∠C.根据SAS证△ABE≌△ACD,推出∠B=∠C即可.
(2):①如果AE=AD,AB=AC,那么OB=OC.②如果AE=AD,∠B=∠C,那么AB=AC.③如果OB=OC,∠B=∠C,那么AE=AD,答案不唯一.
点评:本题考查了全等三角形的性质和判定,命题和定理,主要考查学生的分析问题和解决问题的能力,题目比较典型,答案不唯一.
证明:在△ABE和△ACD中,
∵
 ,
,∴△ABE≌△ACD,
∴∠B=∠C.
(2)解:①如果AE=AD,AB=AC,那么OB=OC.
②如果AE=AD,∠B=∠C,那么AB=AC.
③如果OB=OC,∠B=∠C,那么AE=AD.
分析:(1)如果AE=AD,AB=AC,那么∠B=∠C.根据SAS证△ABE≌△ACD,推出∠B=∠C即可.
(2):①如果AE=AD,AB=AC,那么OB=OC.②如果AE=AD,∠B=∠C,那么AB=AC.③如果OB=OC,∠B=∠C,那么AE=AD,答案不唯一.
点评:本题考查了全等三角形的性质和判定,命题和定理,主要考查学生的分析问题和解决问题的能力,题目比较典型,答案不唯一.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 23、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC:④∠B=∠C.现请你选取其中的三个,以某两个作为已知条件,另一个作为结论.
23、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC:④∠B=∠C.现请你选取其中的三个,以某两个作为已知条件,另一个作为结论.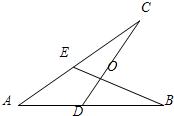 21、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中的三个,以两个作为已知条件,另一个作为结论组成命题.
21、如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中的三个,以两个作为已知条件,另一个作为结论组成命题.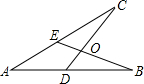 如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.
如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.现选取其中的三个,以两个作为已知条件,另一个作为结论.