题目内容
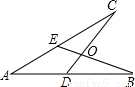
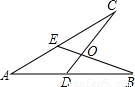
(2010•龙湖区模拟)如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC:④∠B=∠C.现请你选取其中的三个,以某两个作为已知条件,另一个作为结论.(1)试写出一个正确的命题,并加以证明;
(2)请你写出三个正确命题.
【答案】分析:此题是一道开放性的题,我们可以利用全等三角形的判定方法进行解答.例如,已知AE=AD,AB=AC,求证∠B=∠C,我们就可以利用SAS判定△ABE≌△ACD从而得到∠B=∠C.
同样道理,可写出其它的三个正确命题.
解答:解:(1)如果AE=AD,AB=AC,那么∠B=∠C.
证明:在△ABE和△ACD中,
∵AE=AD,∠A=∠A,AB=AC,
∴△ABE≌△ACD,
∴∠B=∠C.
(2)①如果AE=AD,AB=AC,那么OB=OC.
②如果AE=AD,∠B=∠C,那么AB=AC.
③如果OB=OC,∠B=∠C,那么AE=AD.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有AAS,SAS,SSS,HL等.选择条件时要避开SSA与AAA.这两种不能作为三角形全等的判定方法加以应用.
同样道理,可写出其它的三个正确命题.
解答:解:(1)如果AE=AD,AB=AC,那么∠B=∠C.
证明:在△ABE和△ACD中,
∵AE=AD,∠A=∠A,AB=AC,
∴△ABE≌△ACD,
∴∠B=∠C.
(2)①如果AE=AD,AB=AC,那么OB=OC.
②如果AE=AD,∠B=∠C,那么AB=AC.
③如果OB=OC,∠B=∠C,那么AE=AD.
点评:此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有AAS,SAS,SSS,HL等.选择条件时要避开SSA与AAA.这两种不能作为三角形全等的判定方法加以应用.

练习册系列答案
相关题目
 的所有点P的坐标.
的所有点P的坐标.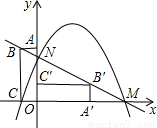
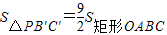 的所有点P的坐标.
的所有点P的坐标.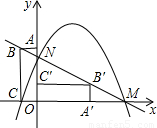
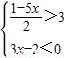 的解集的情况为( )
的解集的情况为( )
