题目内容
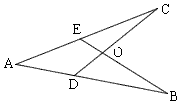
 如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题,并加以证明:①AE=AD;②AB=AC;③BE=CD;④∠B=∠C.
如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题,并加以证明:①AE=AD;②AB=AC;③BE=CD;④∠B=∠C.已知:如图,
AE=AD,AB=AC
AE=AD,AB=AC
求证:
BE=CD
BE=CD
(写序号即可)证明:
∵在△AEB和△ADC中
,
∴△ABE≌△ACD(SAS),
∴BE=CD.
|
∴△ABE≌△ACD(SAS),
∴BE=CD.
∵在△AEB和△ADC中
,
∴△ABE≌△ACD(SAS),
∴BE=CD.
.
|
∴△ABE≌△ACD(SAS),
∴BE=CD.
分析:此题是一个开放题,可以有几个情况:①②→③或④,①④→②或③,②④→①或③,③④→①或②;根据条件:①AE=AD;②AB=AC,∠A=∠A可利用SAS证明△ABE≌△ACD,再根据全等三角形对应边相等可得③BE=CD.
解答:解:①②→③或④,①④→②或③,②④→①或③,③④→①或②;
①②→③理由如下:
∵在△AEB和△ADC中,
,
∴△ABE≌△ACD (SAS),
∴BE=CD.
①②→③理由如下:
∵在△AEB和△ADC中,
|
∴△ABE≌△ACD (SAS),
∴BE=CD.
点评:此题主要考查了全等三角形全等的判定与性质,是一个很好的开放题,关键是掌握证明三角形全等的判定方法SSS、SAS、AAS、ASA.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
相关题目


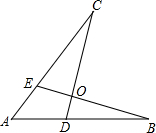 如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题,并加以证明:①AE=AD;②AB=AC;③BE=CD;④∠B=∠C.
如图,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题,并加以证明:①AE=AD;②AB=AC;③BE=CD;④∠B=∠C.