题目内容
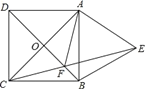
【题目】如图,小军(AB)、小丽(CD)和小红(EF)同时站在路灯下的笔直路线上,其中小丽和小红的影子分别是BD和FM.
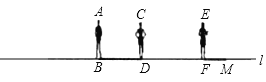
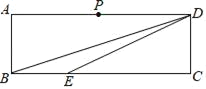
(1)请你在图中画出路灯灯泡所在的位置(用点P表示),并画出小军AB此时在路灯下的影子(用线段BN表示).
(2)若小丽和小红身高都是1.7米,小军身高1.8米,BD=2米,DF=3米,FM=1米,求路灯高度和小军影长,
【答案】(1)见解析;(2)路灯PG的高度为3.4米,小军的影长为4.5米.
【解析】
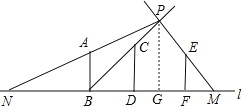
(1)连接BC、ME,并延长BC和ME,两者的交点即为路灯灯泡点P所在的位置;再连接PA,并延长与地面相交的交点即为点N,BN则为小军AB此时在路灯下的影子;
(2)如(1)中的图,过点P作![]() 于点G,根据三角形一边的平行线的性质定理得
于点G,根据三角形一边的平行线的性质定理得![]() ,通过前两个等式先求出
,通过前两个等式先求出![]() (即路灯的高度)的值,再通过第三个式子可求小军的影长BN.
(即路灯的高度)的值,再通过第三个式子可求小军的影长BN.
(1)连接BC、ME,并延长BC和ME,两者的交点即为路灯灯泡点P所在的位置;再连接PA,并延长与地面相交,交点即为点N,BN则为小军AB此时在路灯下的影子,画图如下:
(2)如(1)中的图,过点P作![]() 于点G
于点G
![]()
![]() (三角形一边的平行线的性质定理)
(三角形一边的平行线的性质定理)
设![]() ,
,
则![]()
![]()
解得:![]()
![]()
由![]() 可得:
可得:![]()
解得:![]()
答:路灯PG的高度为3.4米,小军的影长为4.5米.

【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
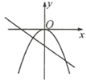
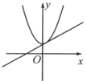
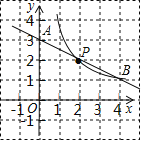
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).