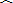题目内容
空投物资用的某种降落伞的轴截面如图所示,△ABG是等边三角形,C、D是以AB为直径的半圆O的两个三等分点,CG、DG分别交AB于点E、F,试判断 点E、F分别位于所在线段的什么位置?并证明你的结论(证明一种情况即可).
点E、F分别位于所在线段的什么位置?并证明你的结论(证明一种情况即可).
 点E、F分别位于所在线段的什么位置?并证明你的结论(证明一种情况即可).
点E、F分别位于所在线段的什么位置?并证明你的结论(证明一种情况即可).答:点E、F均为所在线段的三等分点.
连接OC,设圆的半径长是r,则AB=AG=2r.
∵∠COA=60°,∠GAB=60°,
∴OC∥AG,
∴△AEG∽△OEC,
∴OE:AE=CO:AG=r:2r=1:2,
又∵OE=OF=
EF
∴EF:AE=1:1,
同理可证:BF:FE=1:1,
故AE=EF=FB,即点E、F均为所在线段的三等分点,.
连接OC,设圆的半径长是r,则AB=AG=2r.
∵∠COA=60°,∠GAB=60°,
∴OC∥AG,
∴△AEG∽△OEC,
∴OE:AE=CO:AG=r:2r=1:2,
又∵OE=OF=
| 1 |
| 2 |
∴EF:AE=1:1,
同理可证:BF:FE=1:1,
故AE=EF=FB,即点E、F均为所在线段的三等分点,.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目