Question

【题目】探究：
（1）如图1，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，且MN=DM．设OM=a，请你利用基本活动经验直接写出点N的坐标（用含a的代数式表示）；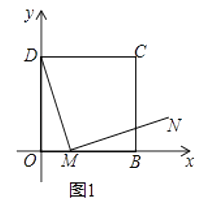

（2）如果（1）的条件去掉“且MN=DM”，加上“交∠CBE的平分线与点N”，如图2，求证：MD=MN．如何突破这种定势，获得问题的解决，请你写出你的证明过程．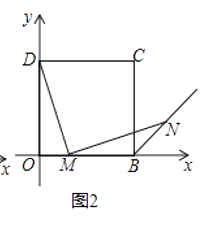

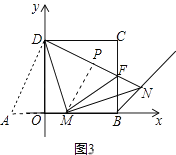
（3）如图3，请你继续探索：连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，请你指出正确的结论，并给出证明．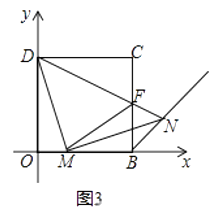

Answer 1

【答案】
（1）N（2+a,a）
（2）证明：如图2中，在OD上取OH=OM，连接HM，

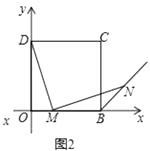
∵OD=OB，OH=OM，

∴HD=MB，∠OHM=∠OMH，

∴∠DHM=180°﹣45°=135°，

∵NB平分∠CBE，

∴∠NBE=45°，

∴∠NBM=180°﹣45°=135°，

∴∠DHM=∠NBM，

∵∠DMN=90°，

∴∠DMO+∠NMB=90°，

∵∠HDM+∠DMO=90°，

∴∠HDM=∠NMB，

在△DHM和△MBN中，

，

∴△DHM≌△MBN（ASA），

∴DM=MN．

（3）解：结论：MN平分∠FMB成立．

证明：如图3中，在BO延长线上取OA=CF，

在△AOD和△FCD中，

，

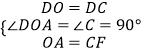∴△DOA≌△DCF，

∴AD=DF，∠ADO=∠CDF，

∵∠MDN=45°，

∴∠CDF+∠ODM=45°，

∴∠ADO+∠ODM=45°，

∴∠ADM=∠FDM，

在△DMA和△DMF中，

，

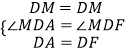∴△DMA≌△DMF，

∴∠DFM=∠DAM=∠DFC，

过M作MP⊥DN于P，则∠FMP=∠CDF，

由（2）可知∠NMF+∠FMP=∠PMN=45°，

∴∠NMB=∠MDH，∠MDO+∠CDF=45°，

∴∠NMB=∠NMF，即MN平分∠FMB．

【解析】解：（1）如图1中，作NE⊥OB于E，

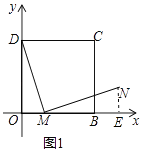
∵∠DMN=90°，

∴∠DMO+∠NME=90°，∠NME+∠MNE=90°，

∴∠DMO=∠MNE，

在△DMO和△MNE中，

，

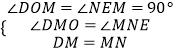∴△DMO≌△MNE，

∴ME=DO=2，NE=OM=a，

∴OE=OM+ME=2+a，

∴点N坐标（2+a，a），

所以答案是N（2+a，a）