题目内容
【题目】如图,已知等腰△ABC中,∠BAC=30°,AB=AC,∠PAB=α,点B关于直线AP的对称点为点D,连接AD,连接BD交AP于点G,连接CD交AP于点E,交AB于点F.
(1)如图当α=15°时,①按要求画出图形,②求出∠ACD的度数,③探究DE与BF的倍数关系并加以证明;
(2)在直线AP绕点A顺时针旋转的过程中(0°<α<75°),当△AEF为等腰三角形时,画出相应图形直接求出α的值为________.

【答案】(1)①见解析;②∠ACD=60°;③DE=2BF,理由见解析;(2)30°或52.5°.
【解析】
(1)①按要求画出即可;
②根据点B关于直线AP的对称点为点D,得到AP垂直平分BD,利用垂直平分线的性质,证明△ACD为等边三角形,即可得到∠ACD=60°;
③DE=2BF,连接EB,根据AP垂直平分BD,得到ED=EB,利用等边对等角得到∠3=∠4,利用等腰三角形的性质求出∠3=∠4=15°,∠5=30°,又因为AD=AC,AB平分∠DAC,所以AB⊥DC,即可得到EB=2BF,所以ED=2BF;
(2)画出图形,分三种情况讨论:当AE=AF时;当AE=EF时;当EF=AF时.
(1)①如图为所求作的图形;
②∵ B、D关于AP对称,
∴AP垂直平分BD,AD=AB,∠1=∠2=15°,
∴∠DAC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°;
③ DE=2BF ,理由如下:
连接 EB,
∴ED=EB,
∵AB=AD,∠DAB=30°,
∴∠ADB=75°,
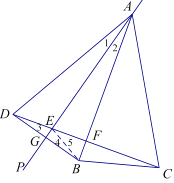
又∵∠ADC=60°,
∴∠3=∠4=15°,
∴∠5=30°,
∵AD=AC ,
AB平分∠DAC ,
∴AB⊥DC ,
∴EB=2BF,
∴ED=2BF ;
(2)如图2,
∵AD=AC,
∴△DAC是等腰三角形,
∴∠ADC=(180°-2α-30°)÷2=75°-α,
∴∠AEF=∠ADC+∠DAE=75°-α+α=75°,
当AE=AF时,∠EAF=α=180°-75°×2=180°-150°=30°;
当AE=EF时,∠EAF=α=(180°-75°)÷=52.5°;
当EF=AF时,∠AEF=∠EAF=a=75°(舍去),
故答案为:30°或52.5°.