题目内容
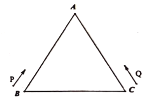
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
【答案】25
【解析】
由题意可知等边三角形![]() 中,P、Q第一次相遇的总路程和为20cm,而后从相遇点到下一次相遇的总路程和为30cm,相遇时间也在每一阶段保持不变,据此进行分析计算.
中,P、Q第一次相遇的总路程和为20cm,而后从相遇点到下一次相遇的总路程和为30cm,相遇时间也在每一阶段保持不变,据此进行分析计算.
解:P、Q第一次相遇用时1s,相遇点在AB上,距离B为6cm;
P、Q第二次相遇用时![]() s,相遇点在AC上,距离A为5cm;
s,相遇点在AC上,距离A为5cm;
P、Q第三次相遇用时![]() s,相遇点在BC上,距离C为4cm;
s,相遇点在BC上,距离C为4cm;
P、Q第四次相遇用时![]() s,相遇点在AB上,距离B为3cm;
s,相遇点在AB上,距离B为3cm;
继续推出可知:
P、Q第一次在三角形![]() 的顶点处相遇,即为第七次相遇时:
的顶点处相遇,即为第七次相遇时:![]() ;
;
P、Q第二次在顶点处相遇,即为第十七次相遇时:![]() .
.
故答案为:25.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】在一次数学社团活动中,指导老师给同学们提出了以下问题:
问题:有67张卡片叠在一起,按从上而下的顺序先把第一张拿走,把第二张放到底层,然后把第三张拿走,再把第四张放到底层,如此进行下去,直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片?
由于卡片数量较多,指导老师建议同学们先对较少的张数进行尝试,以便熟悉游戏规则并发现一些规律!
(1)请你试着在草稿纸上进行试验,将试验结果填写在下表中:
试验的卡片数量 (张) | 2 | 4 | 8 | 9 | 10 | 11 |
剩下最后一张卡片是 原来卡片的第几张 |
(2)根据试验结果的规律,回答最初的67张卡片情形,请你给出答案并简要说明理由.
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?