题目内容
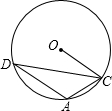 如图,A是⊙O上一点,半径OC等于2,若∠ACD=45°,则弦AD的长是________.
如图,A是⊙O上一点,半径OC等于2,若∠ACD=45°,则弦AD的长是________.
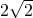
分析:连接OA、OD.构造直角三角形AOD,然后在直角三角形AOD中利用勾股定理求弦AD的长度.
解答:
 解:连接OA、OD.
解:连接OA、OD.∵∠ACD=45°,
∴∠AOD=90°(同弧所对的圆周角等于它所对的圆心角的一半);
又∵⊙O的半径是2,
∴OA=OD=OC=2,
∴在直角三角形中,AD=2
 ;
;故答案是:2
 .
.点评:本题考查了圆周角定理、勾股定理.解答此题时,借助于辅助线OD、OA,构造直角三角形AOD是解题的关键所在.

练习册系列答案
相关题目
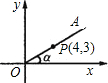 如图,P是OA上一点,且P的坐标为(4,3),则sina和cosa的值分别是( )
如图,P是OA上一点,且P的坐标为(4,3),则sina和cosa的值分别是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
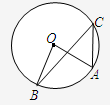 3、如图,C是⊙O上一点,O为圆心,若∠C=40°,则∠AOB为( )
3、如图,C是⊙O上一点,O为圆心,若∠C=40°,则∠AOB为( )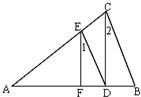 19、如图,E是AC上一点,EF⊥AB于点F,CD⊥AB于点D,∠1=∠2,
19、如图,E是AC上一点,EF⊥AB于点F,CD⊥AB于点D,∠1=∠2, 如图,D是BC上一点,AB=AD,BC=DE.
如图,D是BC上一点,AB=AD,BC=DE. 如图,E是BC上一点,AB⊥BC,且AB=BC,过B点作BD⊥AE于O点,CD∥AE,在以下两个结论中,选择正确的一个结论,并加以证明.
如图,E是BC上一点,AB⊥BC,且AB=BC,过B点作BD⊥AE于O点,CD∥AE,在以下两个结论中,选择正确的一个结论,并加以证明.