Question

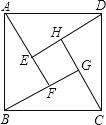
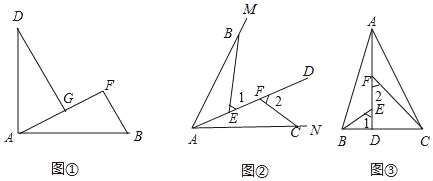
【题目】（1）感知：如图①．AB=AD，AB⊥AD，BF⊥AF于点F，DG⊥AF于点G．求证：△ADG≌△BAF；

（2）拓展：如图②，点B，C在∠MAN的边AM，AN上，点E，F在∠MAN在内部的射线AD上，∠1，∠2分别是△ABE，△CAF的外角，已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；

（3）应用：如图③，在△ABC中，AB=AC，AB＞BC，点在D边BC上，CD=2BD，点E，F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为12，则△ABE与△CDF的面积之和为　 　．

Answer 1

【答案】（1）证明见解析（2）证明见解析（3）8

【解析】

（1）根据同角的余角相等得到∠DAG=∠B，利用AAS定理证明△ADG≌△BAF；

（2）证明∠ABE=∠CAF，利用AAS定理证明△ADG≌△BAF；

（3）根据三角形的面积公式求出S△ADC，根据全等三角形的性质，结合图形计算即可．

（1）证明：∵AB⊥AD，BF⊥AF，

∴∠DAG+∠BAF=90°，∠B+∠BAF=90°，

∴∠DAG=∠B，

在△ADG和△BAF中，

，

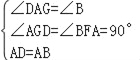∴△ADG≌△BAF（AAS）；

（2）∵∠1=∠2，

∴∠AEB=∠CFA，

∠1=∠ABE+∠BAE，∠BAC=∠CAF+∠BAE，∠1=∠BAC，

∴∠ABE=∠CAF，

在△ABE和△CAF中，

，

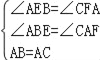∴△ABE≌△CAF（AAS）；

（3）∵CD=2BD，

∴S△ADC=S△ABC=8，

由（2）得，△ABE≌△CAF，

∴△ABE与△CDF的面积之和=△CAF与△CDF的面积之和=S△ADC=8，

故答案为：8．