题目内容
（2006•厦门模拟）如图，AB是斜靠在墙壁上的固定爬梯，梯脚B到墙脚C的距离1.6m，梯上一点D到墙面的距离1.4m，BD长0.5m，则梯子的长为（ ）分析：可由平行线分线段成比例建立线段之间的关系，进而求解线段AB的长度即可．
解答：解：因为梯子每一条踏板均和地面平行，所以构成一组相似三角形，
即△ABC∽△ADE，则
=
，
设梯子长为x米，则
=
，
解得，x=4（m）．
故选：B．
即△ABC∽△ADE，则
| DE |
| BC |
| AD |
| AB |
设梯子长为x米，则
| x-0.5 |
| x |
| 1.4 |
| 1.6 |
解得，x=4（m）．
故选：B．
点评：本题考查了相似三角形在测量高度时的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2006•厦门模拟）下列几个函数图象可能如图所示的是函数（ ）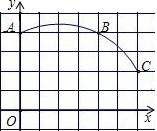
（2006•厦门模拟）如图，在平面直角坐标系中，一条圆弧经过正方形网格格点A，B，C，其中点B（4，4），则该圆弧所在圆的圆心坐标为