题目内容
 (2013•盘锦)如图,点A(1,a)在反比例函数y=
(2013•盘锦)如图,点A(1,a)在反比例函数y=| 3 |
| x |
| k |
| x |
(1)求点A的坐标;
(2)求k值.
分析:(1)把点A(1,a)代入反比例函数y=
可求出a,则可确定A点坐标;
(2)根据平移的性质得到D点坐标为(3,3),然后把D(3,3)代入y=
即可求出k.
| 3 |
| x |
(2)根据平移的性质得到D点坐标为(3,3),然后把D(3,3)代入y=
| k |
| x |
解答:解:(1)把点A(1,a)代入反比例函数y=
(x>0)得a=3,则A点坐标为(1,3),
(2)因为将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,
所以D点坐标为(3,3),
把D(3,3)代入y=
得k=3×3=9.
| 3 |
| x |
(2)因为将△ABO沿x轴向右平移2个单位长度,得到Rt△DEF,
所以D点坐标为(3,3),
把D(3,3)代入y=
| k |
| x |
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k≠0)图象上点的横纵坐标之积为k.也考查了坐标与图形变化-平移.
| k |
| x |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

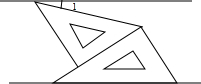 (2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
(2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )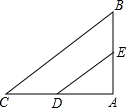 (2013•盘锦)如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
(2013•盘锦)如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( ) (2013•盘锦)如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是
(2013•盘锦)如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是