题目内容
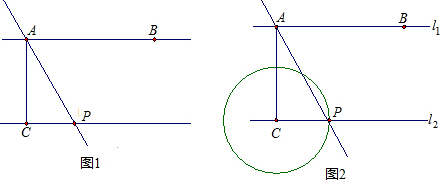
如图1,已知l1∥l2,点A、B在直线l1上,AB=4,过点A作AC⊥l2,垂足为C,AC=3.过点A的直线与直线l2交于点P,以点C为圆心,CP为半径作圆C(如图2).(1)当CP=1时,求cos∠CAP的值;
(2)如果圆C与以点B为圆心,BA为半径的圆B相切,求CP的长;
(3)探究:当直线AP处于什么位置时(只要求出CP的长),将圆C沿着直线AP翻折后得到的圆C′恰好与直线l2相切?并证明你的结论.
分析:(1)根据锐角三角函数的性质,求出AP=
,即可得出cos∠CAP;
(2)利用相切两圆的性质,得出即可;
(3)利用圆C'与直线相切,C'P⊥CP,且C'P=CP; 即∠CPA=45°; 所以CP=AC=3,即可得出答案.
| 10 |
(2)利用相切两圆的性质,得出即可;
(3)利用圆C'与直线相切,C'P⊥CP,且C'P=CP; 即∠CPA=45°; 所以CP=AC=3,即可得出答案.
解答:解:(1)∵AC=3,CP=1,AC⊥CP,
∴AP=
,
∴cos∠CAP=
=
=
;
(2)∵圆C与以点B为圆心,BA为半径的圆B相内切,
AB=4,AC=3,
∴B、C为圆心
∴BC=5
CP=5+4=9;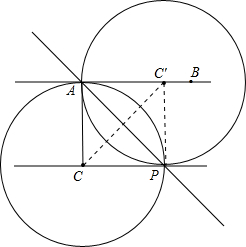
圆C与以点B为圆心,BA为半径的圆B相外切,
AB=4,AC=3,
∴B、C为圆心
∴BC=5
CP=5-4=1,
(3)∵将圆C沿着直线AP翻折后得到的圆C′恰好与直线l2相切,
∴CC'⊥AP; 圆C'与直线相切,C'P⊥CP,且C'P=CP; 即∠CPA=45°; 所以CP=AC=3.
∴当线段CP的长为3时,将圆C沿着直线AP翻折后得到的圆C′恰好与直线l2相切.
∴AP=
| 10 |
∴cos∠CAP=
| AC |
| AP |
| 3 | ||
|
3
| ||
| 10 |
(2)∵圆C与以点B为圆心,BA为半径的圆B相内切,
AB=4,AC=3,
∴B、C为圆心
∴BC=5
CP=5+4=9;

圆C与以点B为圆心,BA为半径的圆B相外切,
AB=4,AC=3,
∴B、C为圆心
∴BC=5
CP=5-4=1,
(3)∵将圆C沿着直线AP翻折后得到的圆C′恰好与直线l2相切,
∴CC'⊥AP; 圆C'与直线相切,C'P⊥CP,且C'P=CP; 即∠CPA=45°; 所以CP=AC=3.
∴当线段CP的长为3时,将圆C沿着直线AP翻折后得到的圆C′恰好与直线l2相切.
点评:此题主要考查了切线的性质和勾股定理以及锐角三角函数的定义等知识,根据已知灵活应用切线的性质定理是解决问题的关键.

练习册系列答案
相关题目

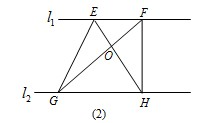
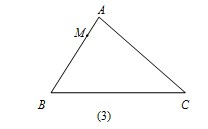
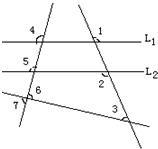 3、如图,若已知L1∥L2,则图中∠1至∠7中相等的角有( )
3、如图,若已知L1∥L2,则图中∠1至∠7中相等的角有( )