题目内容
（本题满分12分，任选一题作答．）
Ⅰ、如图①，在平面直角坐标系中，O为坐标原点，边长为5的正三角形OAB的OA边在x轴的正半轴上．点C、D同时从点O出发，点C以1单位长/秒的速度向点A运动，点D以2个单位长/秒的速度沿折线OBA运动．设运动时间为t秒，0＜t＜5．
（1）当0＜t＜
时，证明DC⊥OA；
（2）若△OCD的面积为S，求S与t的函数关系式；
（3）以点C为中心，将CD所在的直线顺时针旋转60°交AB边于点E，若以O、C、E、D为顶点的四边形是梯形，求点E的坐标．
Ⅱ、（1）如图Ⅱ-1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图Ⅱ-2，已知l1∥l2，点E，F在l1上，点G，H在l2上，试说明△EGO与△FHO面积相等．
（3）如图Ⅱ-3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．
Ⅰ、如图①，在平面直角坐标系中，O为坐标原点，边长为5的正三角形OAB的OA边在x轴的正半轴上．点C、D同时从点O出发，点C以1单位长/秒的速度向点A运动，点D以2个单位长/秒的速度沿折线OBA运动．设运动时间为t秒，0＜t＜5．
（1）当0＜t＜
| 5 | 2 |
（2）若△OCD的面积为S，求S与t的函数关系式；
（3）以点C为中心，将CD所在的直线顺时针旋转60°交AB边于点E，若以O、C、E、D为顶点的四边形是梯形，求点E的坐标．
Ⅱ、（1）如图Ⅱ-1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图Ⅱ-2，已知l1∥l2，点E，F在l1上，点G，H在l2上，试说明△EGO与△FHO面积相等．
（3）如图Ⅱ-3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．
分析：Ⅰ、（1）当0＜t＜
时，点C不过OA中点，想证明垂直应先作出一条和CD有关的垂线，利用相似求解；
（2）应分当0＜t＜
时，和
≤t＜5时两种情况探讨，应用t表示利用特殊的三角函数表示出OC边上的高．进而表示出面积即可．
（3）以O、C、E、D为顶点的四边形是梯形，那么应根据（1）（2）中的两种类型的三角形，可分DE∥CO、CD∥OE两种情况进行探讨；
Ⅱ、（1）根据三角形的面积公式，只需过点A和BC的中点画直线即可；
（2）结合平行线间的距离相等和三角形的面积公式即可证明；
（3）结合（1）和（2）的结论进行求作．
| 5 |
| 2 |
（2）应分当0＜t＜
| 5 |
| 2 |
| 5 |
| 2 |
（3）以O、C、E、D为顶点的四边形是梯形，那么应根据（1）（2）中的两种类型的三角形，可分DE∥CO、CD∥OE两种情况进行探讨；
Ⅱ、（1）根据三角形的面积公式，只需过点A和BC的中点画直线即可；
（2）结合平行线间的距离相等和三角形的面积公式即可证明；
（3）结合（1）和（2）的结论进行求作．
解答：Ⅰ
、解：（1）作BG⊥OA于G．
在Rt△OBG中，
=cos∠BOA=cos60°=
，
而
=
，
∴
=
，
又∵∠DOC=∠BOG，
∴△DOC∽△BOG，
∴∠DCO=∠BGO=90°．
即DC⊥OA；
（2）当0＜t＜
时，
在Rt△OCD中，CD=OD×sin60°=2t×
=
t，
∴S=
×OC×CD=
×t×
t=
t2；
当
≤t＜5时（如图2）
过点D作DH⊥OA于H．
在Rt△AHD中，
HD=AD×sin60°=（10-2t）×
=
（5-t），
S=
×OC×HD=
×t×
（5-t）=
t-
t2；
（3）当DE∥OC时，△DBE是等边三角形．（如图3）
BE=BD=5-2t．
在△CAE中，∠ECA=90°-∠DCE=30°，∠BAO=60°，
∴∠CEA=90°．
而AC=5-t，∴AE=
AC=
，
∴BE+AE=（5-2t）+
=5，
∴t=1，
因此AE=
=2．
过点E作EM⊥OA于M．
则EM=AE×sin60°=2×
=
，
AM=AE×cos60°=2×
=1，OM=OA-AM=4．
∴点E的坐标为（4，
）；
当CD∥OE时（如图4），BD=2t-5．
∠OEA=90°，∴CD⊥AB．
而△OAB是等边三角形，
∴DE=BD-
AB=
，
∴2t-5=
，
∴t=
，
因此AE=
=
，
∴E的纵坐标为
×
=
，
横坐标为5-
×
=
，
∴点E的坐标为（
，
）；
综上所述，点E的坐标为（4，
）或（
，
）；
Ⅱ、（1）解：取BC的中点D，过A、D画直线，则直线AD为所求；
（2）证明：∵l1∥l2，
∴点E，F到l2之间的距离都相等，设为h．
∴S△EGH=
GH•h，S△FGH=
GH•h，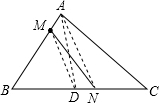
∴S△EGH=S△FGH，
∴S△EGH-S△GOH=S△FGH-S△GOH，
∴△EGO的面积等于△FHO的面积；
（3）解：取BC的中点D，连接MD，过点A作AN∥MD交BC于点N，过M、N画直线，则直线MN为所求．
、解：（1）作BG⊥OA于G．在Rt△OBG中，
| OG |
| OB |
| 1 |
| 2 |
而
| OC |
| OD |
| 1 |
| 2 |
∴
| OG |
| OB |
| OC |
| OD |
又∵∠DOC=∠BOG，
∴△DOC∽△BOG，
∴∠DCO=∠BGO=90°．
即DC⊥OA；
（2）当0＜t＜
| 5 |
| 2 |
在Rt△OCD中，CD=OD×sin60°=2t×
| ||
| 2 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当
| 5 |
| 2 |
过点D作DH⊥OA于H．
在Rt△AHD中，
HD=AD×sin60°=（10-2t）×
| ||
| 2 |
| 3 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
| ||
| 2 |
（3）当DE∥OC时，△DBE是等边三角形．（如图3）
BE=BD=5-2t．
在△CAE中，∠ECA=90°-∠DCE=30°，∠BAO=60°，
∴∠CEA=90°．
而AC=5-t，∴AE=
| 1 |
| 2 |
| 5-t |
| 2 |
∴BE+AE=（5-2t）+
| 5-t |
| 2 |
∴t=1，
因此AE=
| 5-t |
| 2 |
过点E作EM⊥OA于M．
则EM=AE×sin60°=2×
| ||
| 2 |
| 3 |
AM=AE×cos60°=2×
| 1 |
| 2 |
∴点E的坐标为（4，
| 3 |
当CD∥OE时（如图4），BD=2t-5．
∠OEA=90°，∴CD⊥AB．
而△OAB是等边三角形，
∴DE=BD-
| 1 |
| 2 |
| 5 |
| 2 |
∴2t-5=
| 5 |
| 2 |
∴t=
| 15 |
| 4 |
因此AE=
| 5-t |
| 2 |
| 5 |
| 8 |
∴E的纵坐标为
| 5 |
| 8 |
| ||
| 2 |
5
| ||
| 16 |
横坐标为5-
| 5 |
| 8 |
| 1 |
| 2 |
| 75 |
| 16 |
∴点E的坐标为（
| 75 |
| 16 |
5
| ||
| 16 |
综上所述，点E的坐标为（4，
| 3 |
| 75 |
| 16 |
5
| ||
| 16 |
Ⅱ、（1）解：取BC的中点D，过A、D画直线，则直线AD为所求；
（2）证明：∵l1∥l2，
∴点E，F到l2之间的距离都相等，设为h．
∴S△EGH=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EGH=S△FGH，
∴S△EGH-S△GOH=S△FGH-S△GOH，
∴△EGO的面积等于△FHO的面积；
（3）解：取BC的中点D，连接MD，过点A作AN∥MD交BC于点N，过M、N画直线，则直线MN为所求．
点评：Ⅰ、是一道旋转与运动相结合的大题，并且联系函数与四边形知识，要注意这些知识点间的融会贯通．
Ⅱ、主要是根据三角形的面积公式，知：三角形的中线把三角形的面积等分成了相等的两部分；同底等高的两个三角形的面积相等．
Ⅱ、主要是根据三角形的面积公式，知：三角形的中线把三角形的面积等分成了相等的两部分；同底等高的两个三角形的面积相等．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
是否为定值．若是．请求出该定值；若不是．请说明理由。
是否为定值．若是．请求出该定值；若不是．请说明理由。
是否为定值．若是．请求出该定值；若不是．请说明理由。
是否为定值．若是．请求出该定值；若不是．请说明理由。