题目内容
如图,登山队员在山脚A点测得山顶B的仰角∠CAB=45°,当沿倾斜角为30°的斜坡前进100米到达D点后,又在D点测得山顶B点的仰角为60°,求出高BC(精确到1米).(参考数据: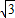 ≈1.732,
≈1.732,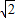 ≈1.414)
≈1.414)
【答案】分析:过点D作DE⊥AC,△ACB是等腰直角三角形,直角△ADE中满足解直角三角形的条件.可以设EC=x,在直角△BDF中,根据勾股定理,可以用x表示出BF,根据AC=BC就可以得到关于x的方程,就可以求出x,得到BC,即可求出山高.
解答: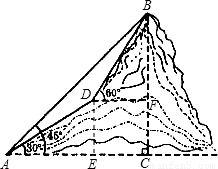 解:过D作DE⊥AC于E,作DF⊥BC于F(1分).
解:过D作DE⊥AC于E,作DF⊥BC于F(1分).
∵∠BAC=45°,∠ACB=90°.
∴∠ABC=45°.(2分)
又∵∠BDF=60°.
∴∠DBF=30°.
∴∠DAB=∠DBA=15°.(3分)
∴DB=DA=100.(4分)
∵∠DAE=30°.
∴FC=DE= AD=50.(5分)
AD=50.(5分)
在△BDF中,sin∠BDF=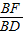 .
.
∴BF=BD×sin∠BDF=100×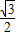 =50
=50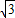 .(6分)
.(6分)
∴山高BC=BF+FC=50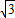 +50≈137(米).(7分)
+50≈137(米).(7分)
点评:本意的难度较大,是根据勾股定理,把问题转化为方程问题.
解答:
 解:过D作DE⊥AC于E,作DF⊥BC于F(1分).
解:过D作DE⊥AC于E,作DF⊥BC于F(1分).∵∠BAC=45°,∠ACB=90°.
∴∠ABC=45°.(2分)
又∵∠BDF=60°.
∴∠DBF=30°.
∴∠DAB=∠DBA=15°.(3分)
∴DB=DA=100.(4分)
∵∠DAE=30°.
∴FC=DE=
 AD=50.(5分)
AD=50.(5分)在△BDF中,sin∠BDF=
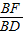 .
.∴BF=BD×sin∠BDF=100×
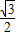 =50
=50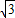 .(6分)
.(6分)∴山高BC=BF+FC=50
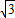 +50≈137(米).(7分)
+50≈137(米).(7分)点评:本意的难度较大,是根据勾股定理,把问题转化为方程问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,登山队员在山脚A点测得山顶B的仰角∠CAB=45°,当沿倾斜角为30°的斜坡前进100米到达D点后,又在D点测得山顶B点的仰角为60°,求出高BC(精确到1米).(参考数据:
如图,登山队员在山脚A点测得山顶B的仰角∠CAB=45°,当沿倾斜角为30°的斜坡前进100米到达D点后,又在D点测得山顶B点的仰角为60°,求出高BC(精确到1米).(参考数据: 如图,登山队员在山脚A点测得山顶B点的仰角为∠CAB=45°,当沿倾斜角为30°的斜坡前进100m到达D点以后,又在D点测得山顶B点的仰角为60°,山的高度BC=
如图,登山队员在山脚A点测得山顶B点的仰角为∠CAB=45°,当沿倾斜角为30°的斜坡前进100m到达D点以后,又在D点测得山顶B点的仰角为60°,山的高度BC= 如图,登山队员在山脚A点测得山顶B的仰角∠CAB=45°,当沿倾斜角为30°的斜坡前进100米到达D点后,又在D点测得山顶B点的仰角为60°,求出高BC(精确到1米).(参考数据:
如图,登山队员在山脚A点测得山顶B的仰角∠CAB=45°,当沿倾斜角为30°的斜坡前进100米到达D点后,又在D点测得山顶B点的仰角为60°,求出高BC(精确到1米).(参考数据: ≈1.732,
≈1.732, ≈1.414)
≈1.414)