题目内容
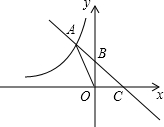 (2012•中江县二模)如图中曲线是反比例函数y=
(2012•中江县二模)如图中曲线是反比例函数y=| m-5 |
| x |
(1)这个反比例函数图象的另一条位于哪个象限?求出常数m的取值范围;
(2)若一次函数y=-
| 2 |
| 5 |
| 4 |
| 5 |
(3)设点M(x0,y0)是线段BC上的一动点,过M作x轴的垂线,垂足为N,作y轴的垂线,垂足为E,求矩形MNOE面积的最大值.
分析:(1)根据反比例函数的性质,当k<0时,图象在第二、四象限,即可得到答案;
(2)首先利用一次函数解析式算出C点坐标,再根据△AOC的面积为2可以得到A点纵坐标,然后再次利用一次函数解析式算出A点横坐标,进而得到A点坐标,再把A点坐标代入反比例函数解析式即可算出m的值;
(3)根据题意画出图形,根据解析式可得y0=-
x0+
,再代入S矩形MNOE=x0y0,可得到S=-
(x02-2x0+1)+
,再利用配方法可得x0=1时矩形MNOE的面积最大.
(2)首先利用一次函数解析式算出C点坐标,再根据△AOC的面积为2可以得到A点纵坐标,然后再次利用一次函数解析式算出A点横坐标,进而得到A点坐标,再把A点坐标代入反比例函数解析式即可算出m的值;
(3)根据题意画出图形,根据解析式可得y0=-
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
解答: 解:(1)∵反比例函数图象的一条在第二象限,
解:(1)∵反比例函数图象的一条在第二象限,
∴这个反比例函数图象的另一条位于第四象限,
∴m-5<0,
∴m<5;
(2)当y=0时,-
x+
=0,x=2,
∴C(2,0),
设A(x1,y1),则S△AOC=
×OC×y1=
×2×y1=2,
∴y1=2,
∴y1=-
x1+
=2,
解得x1=-3,
∴A(-3,2),
把A点坐标代入y=
中得:
2=
,
解得:m=-1;
(3)S矩形MNOE=x0y0=x0(-
x0+
)=-
x02+
x0,
=-
(x02-2x0+1)+
=-
(x0-1)2+
.
∴当M点的横坐标为1时,矩形MNOE的面积最大,最大面积是
.
 解:(1)∵反比例函数图象的一条在第二象限,
解:(1)∵反比例函数图象的一条在第二象限,∴这个反比例函数图象的另一条位于第四象限,
∴m-5<0,
∴m<5;
(2)当y=0时,-
| 2 |
| 5 |
| 4 |
| 5 |
∴C(2,0),
设A(x1,y1),则S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴y1=2,
∴y1=-
| 2 |
| 5 |
| 4 |
| 5 |

解得x1=-3,
∴A(-3,2),
把A点坐标代入y=
| m-5 |
| x |
2=
| m-5 |
| -3 |
解得:m=-1;
(3)S矩形MNOE=x0y0=x0(-
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
=-
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
∴当M点的横坐标为1时,矩形MNOE的面积最大,最大面积是
| 2 |
| 5 |
点评:此题主要考查了反比例函数与一次函数的综合运用,以及三角形的面积公式,关键是熟练掌握反比例函数的性质,熟练掌握函数图象上的点与函数关系式的关系.

练习册系列答案
相关题目
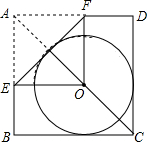 (2012•中江县二模)如图,O是正方形ABCD的对角线AC上一点,⊙O与边BC、CD都相切,点E、F分别在AB、AD上.现将△AEF沿着EF对折,折痕EF与⊙O相切,此时点A恰好落在圆心O处.若AF=4,则四边形ABCD的边长是( )
(2012•中江县二模)如图,O是正方形ABCD的对角线AC上一点,⊙O与边BC、CD都相切,点E、F分别在AB、AD上.现将△AEF沿着EF对折,折痕EF与⊙O相切,此时点A恰好落在圆心O处.若AF=4,则四边形ABCD的边长是( )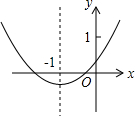 (2012•中江县二模)二次函数y=ax2+bx+c(a≠0)的草图如右.下面的五个结论:①c>1,②2a-b=0,③4ac<b2,④abc<0,⑤9a+3b+c<0.其中正确的有( )
(2012•中江县二模)二次函数y=ax2+bx+c(a≠0)的草图如右.下面的五个结论:①c>1,②2a-b=0,③4ac<b2,④abc<0,⑤9a+3b+c<0.其中正确的有( )