题目内容
 (2012•中江县二模)如图,O是正方形ABCD的对角线AC上一点,⊙O与边BC、CD都相切,点E、F分别在AB、AD上.现将△AEF沿着EF对折,折痕EF与⊙O相切,此时点A恰好落在圆心O处.若AF=4,则四边形ABCD的边长是( )
(2012•中江县二模)如图,O是正方形ABCD的对角线AC上一点,⊙O与边BC、CD都相切,点E、F分别在AB、AD上.现将△AEF沿着EF对折,折痕EF与⊙O相切,此时点A恰好落在圆心O处.若AF=4,则四边形ABCD的边长是( )分析:延长EO交DC于点G,根据折叠对称可以知道OE⊥AB,所以OG⊥CD,即点G是切点,AO交EF于点H,点H是切点.结合图形可知OG=OH=AH=EH,等于⊙O的半径,先求出半径,然后求出正方形的边长.
解答:解:如图:延长EO交DC于点G,则点G是切点,
AO交EF于点H,则点H是切点,
∵四边形ABCD是正方形,点O在对角线AC上,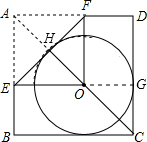
∴AE=OE,OE⊥AB,
∴OG⊥DC,
∴OG=OH=AH=HE=DF,且都等于圆的半径.
在等腰直角三角形AFH中,AF=4,
∴HF=AH=2
=DF.
∴AD=AF+DF=2
+4.
故选D.
AO交EF于点H,则点H是切点,
∵四边形ABCD是正方形,点O在对角线AC上,

∴AE=OE,OE⊥AB,
∴OG⊥DC,
∴OG=OH=AH=HE=DF,且都等于圆的半径.
在等腰直角三角形AFH中,AF=4,
∴HF=AH=2
| 2 |
∴AD=AF+DF=2
| 2 |
故选D.
点评:本题考查的是切线的性质,利用切线的性质,结合正方形的特点求出正方形的边长.

练习册系列答案
相关题目
 (2012•中江县二模)二次函数y=ax2+bx+c(a≠0)的草图如右.下面的五个结论:①c>1,②2a-b=0,③4ac<b2,④abc<0,⑤9a+3b+c<0.其中正确的有( )
(2012•中江县二模)二次函数y=ax2+bx+c(a≠0)的草图如右.下面的五个结论:①c>1,②2a-b=0,③4ac<b2,④abc<0,⑤9a+3b+c<0.其中正确的有( )