Question

如图，CD为Rt△ABC斜边上的高，∠BAC的平分线分别交CD、CB于点E、F，FG⊥AB，垂足为G，则CF    FG，∠1+∠3=    度，∠2+∠4=    度，∠3    ∠4，CE    CF．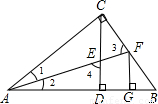

Answer 1

【答案】分析：由于AF平分∠BAC，FC⊥AC，FG⊥AB，根据角平分线定理可得CF=FG；由Rt△ABC可得，∠1+∠3=90°；由CD为Rt△ABC斜边上的高，可得∠2+∠4=90°；由∠1=∠2，得到∠3=∠4；由∠CEF=∠4，而∠3=∠4，于是有∠CEF=∠3，得到CE=CF．
解答：解：（1）∵AF平分∠BAC，FG⊥AB，
而△ABC为Rt△，则FC⊥AC，
∴CF=FG；

（2）∵△ABC为Rt△，
∴∠1+∠3=180°-90°=90°①；
∵CD为Rt△ABC斜边上的高，
∴∠2+∠4=180°-90°=90°②；

（3）∵∠1=∠2，
又由①②得，∠3=∠4；

（4）∵∠CEF=∠4，
而∠3=∠4，
∴∠CEF=∠3，
∴CE=CF．
故答案为=，90，90，=，=．
点评：本题考查了三角形的内角和定理：三角形的三个内角的和为180°．同时考查了角平分线的性质和垂线的性质．