题目内容
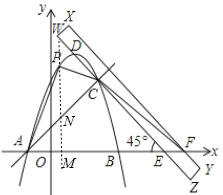
【题目】如图,已知抛物线![]() (a≠0)交x轴与A,B两点(点A在点B左侧),将直尺WXYZ与x轴负方向成45°放置,边WZ经过抛物线上的点C(4,m),与抛物线的另一交点为点D,直尺被x轴截得的线段EF=2,且△CEF的面积为6.
(a≠0)交x轴与A,B两点(点A在点B左侧),将直尺WXYZ与x轴负方向成45°放置,边WZ经过抛物线上的点C(4,m),与抛物线的另一交点为点D,直尺被x轴截得的线段EF=2,且△CEF的面积为6.
(1)求该抛物线的解析式;
(2)探究:在直线AC上方的抛物线上是否存在一点P,使得△ACP的面积最大?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由.
(3)将直尺以每秒2个单位的速度沿x轴向左平移,设平移的时间为t秒,平移后的直尺为W′X′Y′Z′,其中边X′Y′所在的直线与x轴交于点M,与抛物线的其中一个交点为点N,请直接写出当t为何值时,可使得以C、D、M、N为顶点的四边形是平行四边形.

【答案】(1)![]() ;(2)存在一点P(1,
;(2)存在一点P(1,![]() ),使得△ACP的面积最大,面积的最大值为
),使得△ACP的面积最大,面积的最大值为![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)∵S△CEF=![]() EFyC=
EFyC=![]() ×2m=6,∴m=6,即点C的坐标为(4,6),将点C(4,6)代入抛物线
×2m=6,∴m=6,即点C的坐标为(4,6),将点C(4,6)代入抛物线![]() (a≠0)中,得:6=16a+8+6,解得:a=
(a≠0)中,得:6=16a+8+6,解得:a=![]() ,∴该抛物线的解析式为
,∴该抛物线的解析式为![]() ;
;
(2)假设存在.过点P作y轴的平行线,交x轴与点M,交直线AC于点N,如图1所示.
令抛物线![]() 中y=0,则有
中y=0,则有![]() ,解得:
,解得:![]() ,
,![]() ,∴点A的坐标为(﹣2,0),点B的坐标为(6,0).
,∴点A的坐标为(﹣2,0),点B的坐标为(6,0).
设直线AC的解析式为y=kx+b,点P的坐标为(n,![]() )(﹣2<n<4),∵直线AC过点A(﹣2,0)、C(4,6),∴
)(﹣2<n<4),∵直线AC过点A(﹣2,0)、C(4,6),∴![]() ,解得:
,解得:![]() ,∴直线AC的解析式为y=x+2.
,∴直线AC的解析式为y=x+2.
∵点P的坐标为(n,![]() ),∴点N的坐标为(n,n+2).
),∴点N的坐标为(n,n+2).
∵S△ACP=![]() PN(xC﹣xA)=
PN(xC﹣xA)=![]() =
=![]() ,∴当n=1时,S△ACP取最大值,最大值为
,∴当n=1时,S△ACP取最大值,最大值为![]() ,此时点P的坐标为(1,
,此时点P的坐标为(1,![]() ),∴在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为
),∴在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为![]() ,此时点P的坐标为(1,
,此时点P的坐标为(1,![]() ).
).
(3)∵直尺WXYZ与x轴负方向成45°放置,∴设直线CD的解析式为y=﹣x+c,∵点C(4,6)在直线CD上,∴6=﹣4+c,解得:c=10,∴直线CD的解析式为y=﹣x+10.
联立直线CD与抛物线解析式成方程组: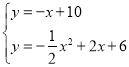 ,解得:
,解得:![]() ,或
,或![]() ,∴点D的坐标为(2,8).
,∴点D的坐标为(2,8).
令直线CD的解析式y=﹣x+10中y=0,则0=﹣x+10,解得:x=10,即点E的坐标为(10,0),∵EF=2,且点E在点F的左边,∴点F的坐标为(12,0).
设点M的坐标为(12﹣2t,0),则点N的坐标为(12﹣2t﹣2,0+2),即N(10﹣2t,2).
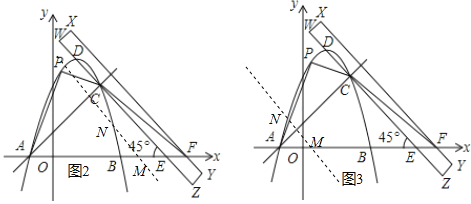
∵点N(10﹣2t,2)在抛物线![]() 的图象上,∴
的图象上,∴![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,
,![]() ,∴当t为
,∴当t为![]() 或
或![]() 秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.
秒时,可使得以C、D、M、N为顶点的四边形是平行四边形.

【题目】二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的对称轴是( )
A.直线x=﹣3
B.直线x=﹣2
C.直线x=﹣1
D.直线x=0