题目内容
 (2013•南昌)如图,在平面直角坐标系中,反比例函数y=
(2013•南昌)如图,在平面直角坐标系中,反比例函数y=| k | x |
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
分析:(1)根据矩形性质得出AB=CD=2,AD=BC=4,即可得出答案;
(2)设矩形平移后A的坐标是(2,6-x),C的坐标是(6,4-x),得出k=2(6-x)=6(4-x),求出x,即可得出矩形平移后A的坐标,代入反比例函数的解析式求出即可.
(2)设矩形平移后A的坐标是(2,6-x),C的坐标是(6,4-x),得出k=2(6-x)=6(4-x),求出x,即可得出矩形平移后A的坐标,代入反比例函数的解析式求出即可.
解答:解:(1)∵四边形ABCD是矩形,平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
∴AB=CD=2,AD=BC=4,
∴B(2,4),C(6,4),D(6,6);
(2)A、C落在反比例函数的图象上,
设矩形平移后A的坐标是(2,6-x),C的坐标是(6,4-x),
∵A、C落在反比例函数的图象上,
∴k=2(6-x)=6(4-x),
x=3,
即矩形平移后A的坐标是(2,3),
代入反比例函数的解析式得:k=2×3=6,
即A、C落在反比例函数的图象上,矩形的平移距离是3,反比例函数的解析式是y=
.
∴AB=CD=2,AD=BC=4,
∴B(2,4),C(6,4),D(6,6);
(2)A、C落在反比例函数的图象上,
设矩形平移后A的坐标是(2,6-x),C的坐标是(6,4-x),
∵A、C落在反比例函数的图象上,
∴k=2(6-x)=6(4-x),
x=3,
即矩形平移后A的坐标是(2,3),
代入反比例函数的解析式得:k=2×3=6,
即A、C落在反比例函数的图象上,矩形的平移距离是3,反比例函数的解析式是y=
| 6 |
| x |
点评:本题考查了矩形性质,用待定系数法求反比例函数的解析式,平移的性质的应用,主要考查学生的计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
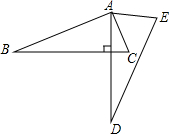 (2013•南昌)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
(2013•南昌)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( ) (2013•南昌)如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( )
(2013•南昌)如图,正六边形ABCDEF中,AB=2,点P是ED的中点,连接AP,则AP的长为( ) (2013•南昌)如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为
(2013•南昌)如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为 (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.