Question

已知等腰三角形顶角是底角的10倍，腰长为10cm，那么这个三角形腰上的高为________．

Answer 1

5cm
分析：根据三角形的内角和定理求出底角的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和求出与顶角相邻的外角的度数是30°，然后根据30°角所对的直角边等于斜边的一半解答．
解答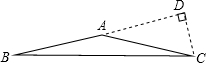：解：如图，设三角形的底角为x，则顶角为10x，
则x+x+10x=180°，
解得x=15°，
即∠B=∠C=15°，
所以，∠CAD=∠B+∠C=15°+15°=30°，
∵腰长AC为10cm，
∴腰上的高CD=AC=×10=5cm．
故答案为：5cm．
点评：本题考查了30°角所对的直角边等于斜边的一半的性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟练掌握各性质定理是解题的关键．