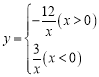��Ŀ����
����Ŀ����ͼ����֪������![]() ��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1��
��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1��
��1����������ߵĽ���ʽ�Լ���B�����꣮
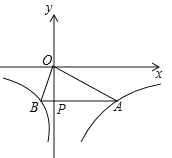
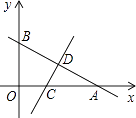
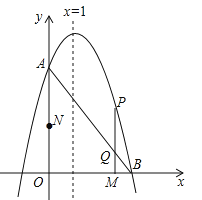
��2������M�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x���������˶���ͬʱ����N�ӵ�O��������ÿ��3����λ���ȵ��ٶ���y���������˶�����N�㵽��A��ʱ��M��Nͬʱֹͣ�˶���������M��x��Ĵ��߽��߶�AB�ڵ�Q�����������ڵ�P�����˶���ʱ��Ϊt�룮
����tΪ��ֵʱ���ı���OMPNΪ���Σ�
����t��0ʱ����BOQ�ܷ�Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
���𰸡���1��![]() ��B������Ϊ��3��0������2����������
��B��������3��0������2����������
��������
�����������1���ɶԳ��ṫʽ�����b����A����������c�������������߽���ʽ������y=0�����B�����ꣻ
��2������t�ɱ�ʾ��ON��OM����ɱ�ʾ��P�����꣬���ɱ�ʾ��PM�ij����ɾ��ε����ʿɵ�ON=PM���ɵõ�����t�ķ��̣������t��ֵ�����������֪OB=OA���ʵ���BOQΪ����������ʱ��ֻ����OB=BQ��OQ=BQ����t�ɱ�ʾ��Q������꣬��ɱ�ʾ��OQ��BQ�ij����ֱ�õ�����t�ķ��̣������t��ֵ��
���������
��1����������![]() �Գ�����ֱ��x=1������
�Գ�����ֱ��x=1������![]() =1�����b=2���������߹�A��0��3������c=3���������߽���ʽΪ
=1�����b=2���������߹�A��0��3������c=3���������߽���ʽΪ![]() ����y=0�ɵ�
����y=0�ɵ�![]() �����x=��1��x=3����B������Ϊ��3��0����
�����x=��1��x=3����B��������3��0����
��2�����������֪ON=3t��OM=2t����P���������ϣ���P��2t��![]() �������ı���OMPNΪ���Σ���ON=PM����3t=
�������ı���OMPNΪ���Σ���ON=PM����3t=![]() �����t=1��t=��
�����t=1��t=��![]() ����ȥ��������t��ֵΪ1ʱ���ı���OMPNΪ���Σ�
����ȥ��������t��ֵΪ1ʱ���ı���OMPNΪ���Σ�
�ڡ�A��0��3����B��3��0������OA=OB=3���ҿ����ֱ��AB����ʽΪy=��x+3������t��0ʱ��OQ��OB��������BOQΪ����������ʱ����OB=QB��OQ=BQ����������������֪OM=2t����Q��2t����2t+3������OQ=![]() =
=![]() ��BQ=
��BQ=![]() =
=![]() |2t��3|�����������֪0��t��1����OB=QBʱ������
|2t��3|�����������֪0��t��1����OB=QBʱ������![]() |2t��3|=3�����t=
|2t��3|=3�����t=![]() ����ȥ����t=
����ȥ����t=![]() ��
��
��OQ=BQʱ������![]() =
=![]() |2t��3|�����t=
|2t��3|�����t=![]() ��
��
���Ͽ�֪��t��ֵΪ![]() ��
��![]() ʱ����BOQΪ���������Σ�
ʱ����BOQΪ���������Σ�