题目内容
【题目】如图,在四边形ABCD中,∠B=90°,过点D作DE∥AB,交BC于E,且DE=BC,连接AC交AC于F,若∠ACB=∠CDE=30°,则图中有几个等腰三角形?请找出来并说明理由. 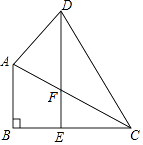
【答案】解:共有两个等腰三角形,分别是△ACD,△DCF.
理由:∵DE∥AB,
∴∠DEC=∠B,
在△DCE和△CAB中,
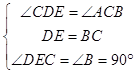 ,
,
∴△DCE≌△CAB,
∴CA=CD,
∴△ACD是等腰三角形,
∵∠B=90°,
∴∠DEC=90°,
∵∠ACB=∠CDE=30°,
∴∠DCE=90°﹣∠CDE=60°,
∴∠DCF=∠DCE﹣∠ACE=30°=∠CDE,
∴DF=CF,
∴△DCF是等腰三角形.
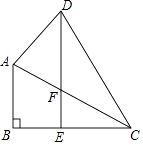
【解析】首先证明△DCE≌△CAB推出CA=CD,再证明∠FCD=∠FDC=30°即可解决问题.
【考点精析】本题主要考查了平行线的性质和等腰三角形的判定的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.

练习册系列答案
相关题目