题目内容
关于x的二次函数y=-x2+(k2-4)x+2k-2以y轴为对称轴,且与y轴的交点在x轴上方.(1)求此抛物线的解析式,并在下面建立直角坐标系画出函数的草图;
(2)设A是y轴右侧抛物线上的一个动点,过点A作AB垂直于x轴于点B,再过点A作x轴的平行线交抛物线于点D,过点D作DC垂直于x轴于点C,得到矩形ABCD.设矩形ABCD的周长为l,点A的横坐标为x,试求l关于x的函数关系式;
(3)当点A在y轴右侧的抛物线上运动时,矩形ABCD能否成为正方形?若能,请求出此时正方形的周长;若不能,请说明理由.
分析:(1)因为二次函数y=-x2+(k2-4)x+2k-2以y轴为对称轴,所以k2-4=0,即可解出k的值,求出抛物线解析式,并利用描点法画出图象;
(2)求出抛物线与x轴的交点坐标,分矩形在x轴上方和矩形在x轴下方两种情况,根据矩形周长公式解答;
(3)假设能构成正方形,根据正方形边长相等,列等式解出x的值,若x>0,则能构成正方形,若x<0,则不能构成正方形.
(2)求出抛物线与x轴的交点坐标,分矩形在x轴上方和矩形在x轴下方两种情况,根据矩形周长公式解答;
(3)假设能构成正方形,根据正方形边长相等,列等式解出x的值,若x>0,则能构成正方形,若x<0,则不能构成正方形.
解答: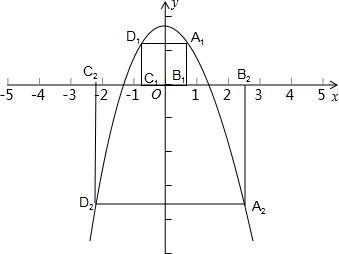 解:
解:
(1)据题意得:k2-4=0,
∴k=±2.
当k=2时,2k-2=2>0.
当k=-2时,2k-2=-6<0(2分)
又∵抛物线与y轴的交点在x轴上方,
∴k=2.
∴抛物线的解析式为:y=-x2+2.(1分)
(2)解:令-x2+2=0,得x=±
.
当0<x<
时,A1D1=2x,A1B1=-x2+2,
∴l=2(A1B1+A1D1)=-2x2+4x+4(2分)
当x>
时,A2D2=2x.
A2B2=-(-x2+2)=x2-2.
∴l=2(A2D2+A2B2)=2x2+4x-4(2分)
(3)当0<x<
时,令A1B1=A1D1,得x2+2x-2=0.
解得x=-1-
(舍去),或x=-1+
.
将x=-1+
代入l=-2x2+4x+4,
得l=8
-8(3分)
当x>
时,令A2B2=A2D2得:x2-2x-2=0,
解得x=1-
(舍去),或x=1+
.
代入l=2x2+4x-4,得L=8
+8(3分)
综上,矩形ABCD能成为正方形,
且当x=
-1时正方形的周长是8
-8,
当x=
+1时,周长为8
+8(1分).
 解:
解:(1)据题意得:k2-4=0,
∴k=±2.
当k=2时,2k-2=2>0.
当k=-2时,2k-2=-6<0(2分)
又∵抛物线与y轴的交点在x轴上方,
∴k=2.
∴抛物线的解析式为:y=-x2+2.(1分)
(2)解:令-x2+2=0,得x=±
| 2 |
当0<x<
| 2 |
∴l=2(A1B1+A1D1)=-2x2+4x+4(2分)
当x>
| 2 |
A2B2=-(-x2+2)=x2-2.
∴l=2(A2D2+A2B2)=2x2+4x-4(2分)
(3)当0<x<
| 2 |
解得x=-1-
| 3 |
| 3 |
将x=-1+
| 3 |
得l=8
| 3 |
当x>
| 2 |
解得x=1-
| 3 |
| 3 |
代入l=2x2+4x-4,得L=8
| 3 |
综上,矩形ABCD能成为正方形,
且当x=
| 3 |
| 3 |
当x=
| 3 |
| 3 |
点评:解答此题的关键是求出二次函数的解析式,利用解析式求出各点的坐标表达式,根据矩形或正方形的性质来解答.值得关注,(3)为探索性问题,有一定的开放性.

练习册系列答案
相关题目
 已知关于x 的一元二次方程(m+2)x2-2x-1=0.
已知关于x 的一元二次方程(m+2)x2-2x-1=0.