题目内容
 (2012•瑶海区二模)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;根据以上操作,若第2012次操作,可得到小正方形的个数是
(2012•瑶海区二模)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;根据以上操作,若第2012次操作,可得到小正方形的个数是6037
6037
.分析:根据第一次可得到4个正方形;第二次可得到4+3=7个正方形;第三次可得到4+2×3=10个正方形;…第n次可得4+(n-1)×3个正方形,进而得出答案即可.
解答:解:∵第一次可得到4个正方形;第二次可得到4+3=7个正方形;第三次可得到4+2×3=10个正方形;…
∴第n次可得4+(n-1)×3个正方形
∴若要操作的2012次,
则4+(2012-1)×3=6037,
故若第2012次操作,可得到小正方形的个数是6037.
故答案为:6037.
∴第n次可得4+(n-1)×3个正方形
∴若要操作的2012次,
则4+(2012-1)×3=6037,
故若第2012次操作,可得到小正方形的个数是6037.
故答案为:6037.
点评:本题主要考查了数字的变化类问题,在解题时要找出题中的规律是解题的关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
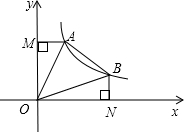 (2012•瑶海区二模)如图,直线y=-x+b(b>0)与双曲线
(2012•瑶海区二模)如图,直线y=-x+b(b>0)与双曲线