题目内容
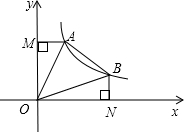 (2012•瑶海区二模)如图,直线y=-x+b(b>0)与双曲线y=
(2012•瑶海区二模)如图,直线y=-x+b(b>0)与双曲线y=| k |
| x |
| 2 |
①②③
①②③
.分析:①②设A(x1,y1),B(x2,y2),联立y=-x+b与y=
,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;
③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
④延长MA,NB交于G点,可证△ABG为等腰直角三角形,当AB=
时,GA=GB=1,则ON-BN=GN-BN=GB=1;
| k |
| x |
③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
④延长MA,NB交于G点,可证△ABG为等腰直角三角形,当AB=
| 2 |
解答:解:设A(x1,y1),B(x2,y2),代入y=
中,得x1•y1=x2•y2=k,
联立
,得x2-bx+k=0,
则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,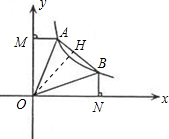
∴ON=OM,AM=BN,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵②△AOM≌△BON,正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=
k+
k=k,正确;
④延长MA,NB交于G点,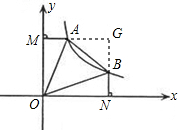
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=
时,GA=GB=1,
∴ON-BN=GN-BN=GB=1,
∴当AB=
时,ON=BN=1不正确.
正确的结论有3个,故答案为①②③.
| k |
| x |
联立
|
则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,

∴ON=OM,AM=BN,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵②△AOM≌△BON,正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=
| 1 |
| 2 |
| 1 |
| 2 |
④延长MA,NB交于G点,

∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=
| 2 |
∴ON-BN=GN-BN=GB=1,
∴当AB=
| 2 |
正确的结论有3个,故答案为①②③.
点评:本题考查了反比例函数的综合运用.关键是明确反比例函数图象上点的坐标特点,反比例函数图象的对称性.

练习册系列答案
相关题目
 (2012•瑶海区二模)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;根据以上操作,若第2012次操作,可得到小正方形的个数是
(2012•瑶海区二模)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;根据以上操作,若第2012次操作,可得到小正方形的个数是