题目内容
(2012•龙岩)如图1,过△ABC的顶点A作高AD,将点A折叠到点D(如图2),这时EF为折痕,且△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG折叠,使B、C两点都与点D重合,得到一个矩形EFGH(如图3),我们称矩形EFGH为△ABC的边BC上的折合矩形.
(1)若△ABC的面积为6,则折合矩形EFGH的面积为
(2)如图4,已知△ABC,在图4中画出△ABC的边BC上的折合矩形EFGH;
(3)如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,BC边上的高AD=
a
a.

(1)若△ABC的面积为6,则折合矩形EFGH的面积为
3
3
;(2)如图4,已知△ABC,在图4中画出△ABC的边BC上的折合矩形EFGH;
(3)如果△ABC的边BC上的折合矩形EFGH是正方形,且BC=2a,那么,BC边上的高AD=
2a
2a
,正方形EFGH的对角线长为| 2 |
| 2 |

分析:(1)根据折叠得出△DEF≌△AEF,△BEH≌△DEH,△CFG≌△DFG,求出矩形EFGH的面积是S△DEF+S△DEH+S△DFG=
S△ABC,代入求出即可;
(2)根据已知和折叠性质,结合图2画出即可;
(3)根据折叠性质得出△AEF边EF上高和△DEF边EF上高相等,DH=BH,DG=GC,求出HG=
BC,根据正方形的性质求出EF=FG=GH=EH=a,即可求出AD,由勾股定理求出正方形EFGH的对角线即可.
| 1 |
| 2 |
(2)根据已知和折叠性质,结合图2画出即可;
(3)根据折叠性质得出△AEF边EF上高和△DEF边EF上高相等,DH=BH,DG=GC,求出HG=
| 1 |
| 2 |
解答:解:(1)∵沿EF折叠A与D重合,
∴△DEF≌△AEF,
∵△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG折叠,使B、C两点都与点D重合,
∴△BEH≌△DEH,△CFG≌△DFG,
∴矩形EFGH的面积是S△DEF+S△DEH+S△DFG=
S△ABC=
×6=3,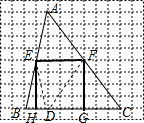
故答案为:3.
(2)如右图所示:
(3)∵根据折叠得出△BEH≌△DEH,△CFG≌△DFG,BC=2a,
∴△AEF边EF上高和△DEF边EF上高相等,DH=BH,DG=GC,
∴HG=
BC=a,
∵四边形EFGH是正方形,
∴EF=FG=GH=EH=a,
则AD=2EH=2a,
由勾股定理得:正方形EFGH的对角线是:
=
a,
故答案为:2a,
a.
∴△DEF≌△AEF,
∵△BED和△CFD都是等腰三角形,再将△BED和△CFD沿它们各自的对称轴EH、FG折叠,使B、C两点都与点D重合,
∴△BEH≌△DEH,△CFG≌△DFG,
∴矩形EFGH的面积是S△DEF+S△DEH+S△DFG=
| 1 |
| 2 |
| 1 |
| 2 |

故答案为:3.
(2)如右图所示:
(3)∵根据折叠得出△BEH≌△DEH,△CFG≌△DFG,BC=2a,
∴△AEF边EF上高和△DEF边EF上高相等,DH=BH,DG=GC,
∴HG=
| 1 |
| 2 |
∵四边形EFGH是正方形,
∴EF=FG=GH=EH=a,
则AD=2EH=2a,
由勾股定理得:正方形EFGH的对角线是:
| a2+a2 |
| 2 |
故答案为:2a,
| 2 |
点评:本题考查了正方形性质、折叠性质、勾股定理的应用,通过做此题培养了学生的观察图形的能力和计算能力,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
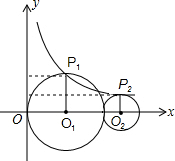 (2012•龙岩)如图,平面直角坐标系中,⊙O1过原点O,且⊙O1与⊙O2相外切,圆心O1与O2在x轴正半轴上,⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直,且点P1(x1,y1)、P2(x2,y2)在反比例函数y=
(2012•龙岩)如图,平面直角坐标系中,⊙O1过原点O,且⊙O1与⊙O2相外切,圆心O1与O2在x轴正半轴上,⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直,且点P1(x1,y1)、P2(x2,y2)在反比例函数y= (2012•龙岩)如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD绕AB所在直线旋转一周所得圆柱的侧面积为( )
(2012•龙岩)如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD绕AB所在直线旋转一周所得圆柱的侧面积为( ) (2012•龙岩)如图,a∥b,∠1=30°,则∠2=
(2012•龙岩)如图,a∥b,∠1=30°,则∠2=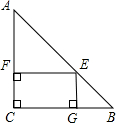 (2012•龙岩)如图,Rt△ABC中,∠C=90°,AC=BC=6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是
(2012•龙岩)如图,Rt△ABC中,∠C=90°,AC=BC=6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是