题目内容
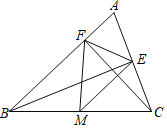
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
【答案】(1)∠EMF=40°;(2)2![]() .
.
【解析】
(1)根据直角三角形的性质得到BM=FM,根据等腰三角形的性质、三角形内角和定理计算;
(2)作MN⊥EF于N,根据直角三角形的性质得到FM=![]() BC=5,根据等腰三角形的性质、三角形面积公式计算.
BC=5,根据等腰三角形的性质、三角形面积公式计算.
解:(1)∵CF⊥AB,M为BC的中点,
∴BM=FM,
∵∠ABC=50°,
∴∠MFB=∠MBF=50°,
∴∠BMF=180°-2×50°=80°,
同理,∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°;
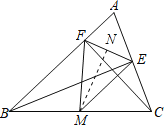
(2)作MN⊥EF于N,
∵CF⊥AB,M为BC的中点,
∴MF是Rt△BFC斜边上的中线,
∴FM=![]() BC=5,
BC=5,
同理可得,ME=5,
∴△EFM是等腰三角形,
∵EF=4,
∴FN=2,
∴MN=![]() =
=![]() ,
,
∴△EFM的面积=![]() EFMN=
EFMN=![]() ×4×
×4×![]() =2
=2![]() .
.

练习册系列答案
相关题目