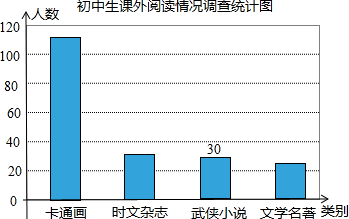
题目内容
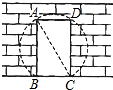 (2012•新昌县模拟)为美化校园,学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门,如图所示,量得矩形门宽为1m,对角线AC的长为2m.
(2012•新昌县模拟)为美化校园,学校决定将花园边墙上的矩形门ABCD改为以AC为直径的圆弧形门,如图所示,量得矩形门宽为1m,对角线AC的长为2m.(1)求原矩形门的面积;
(2)求要打掉的墙体面积.(结果保留л和根号)
分析:(1)在直角三角形ADC中,由AD与AC的长,利用勾股定理求出DC的长,然后利用矩形的面积=长×宽,即可求出矩形ABCD的面积;
(2)打掉墙体的面积=圆O的面积-矩形ABCD的面积,求出即可.
(2)打掉墙体的面积=圆O的面积-矩形ABCD的面积,求出即可.
解答: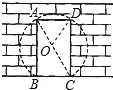 解:(1)∵在Rt△ADC中,AD=1,AC=2,
解:(1)∵在Rt△ADC中,AD=1,AC=2,
根据勾股定理得:DC=
=
m,
∴S矩形ABCD=AD•DC=
m2;
(2)由直径AC=2m,得到半径OA=OC=OD=1m,
∵sin∠ACD=
=
,
∴∠ACD=30°,
则∠AOD=60°,
则S△AOD=
,S扇形AOD=
=
,
则S弓形BC=S弓形AD=
-
则S打掉墙体=S圆O-S矩形ABCD-S弓形BC=π-
-
+
=
-
.
 解:(1)∵在Rt△ADC中,AD=1,AC=2,
解:(1)∵在Rt△ADC中,AD=1,AC=2,根据勾股定理得:DC=
| AC2-AD2 |
| 3 |
∴S矩形ABCD=AD•DC=
| 3 |
(2)由直径AC=2m,得到半径OA=OC=OD=1m,
∵sin∠ACD=
| AD |
| AC |
| 1 |
| 2 |
∴∠ACD=30°,
则∠AOD=60°,
则S△AOD=
| ||
| 4 |
| 60π |
| 360 |
| π |
| 6 |
则S弓形BC=S弓形AD=
| π |
| 6 |
| ||
| 4 |
则S打掉墙体=S圆O-S矩形ABCD-S弓形BC=π-
| 3 |
| π |
| 6 |
| ||
| 4 |
| 5π |
| 6 |
3
| ||
| 4 |
点评:此题考查了垂径定理的应用,勾股定理,等边三角形的性质,以及扇形的面积公式,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目