题目内容
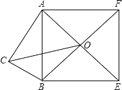
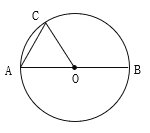
【题目】如图,在⊙O中,AB是直径,半径为R,弧AC=![]() R.
R.
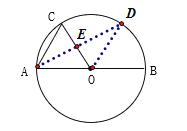
求:(1)∠AOC的度数.(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
【答案】(1)∠AOC=60°;
(2)D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点其中一条.
【解析】
(1)根据弧AC=![]() R和弧长公式
R和弧长公式![]() ,即可求得弧所对的圆心角的度数;
,即可求得弧所对的圆心角的度数;
(2)根据全等三角形的性质得到对应角相等,再根据内错角相等,两条直线平行,即可得到AC∥OD,或者结合(1)的结论发现等边三角形AOC,从而证明点D只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点即可.
解:(1)设∠AOC=n°,
∵AC=![]() R,
R,
∴![]() R
R![]() ,
,
∴n=60°,
∴∠AOC=60°;
(2)∵∠AOC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°.
∵△AEC≌△DEO,
∴∠CAO=∠DOB=∠C=60°,
∴AC∥OD,
∴∠BOD=∠CAO=60°, ∠COD=∠C=60°,
∴D是劣弧BC的中点,
∴D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点即可.

【题目】某校九年级教师在某班随机抽查了学生报考志愿的情况,绘制了如下扇形图和统计表,学生统计表绘制好后不小心撕掉了一个角.
报考学校 | 一中 | 二中 | 八中 | 其他 |
报考人数 | 4 | 5 | 6 |
(1)求撕掉角上的数和抽查学生的总数;
(2)老师打算从抽查的学生中随机抽取1个人来谈感想,求抽到报考一中学生的概率;
(3)把抽查学生的人数看做一组数据,抽查学生报考志愿人数的众数是 ,报考志愿的人数中位数是 .
(4)报考一中的人数百分比在扇形统计图中所占圆心角的正切值为 ,报考八中的百分比所占扇形统计图的圆心角的度数是 .(注:tan36°≈0.7265;tan72°≈3.078;)

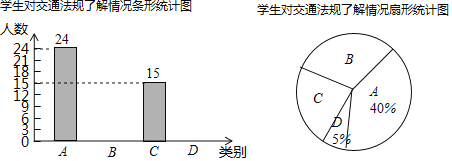
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?