题目内容
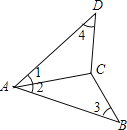
【题目】已知一次函数y=kx+b 的图象与反比例函数y=
的图交象于A、B两点，且点A的横坐标和点B的纵坐标都是－2 ， 求：
（1）一次函数的解析式；
（2）△AOB的面积
【答案】（1）y=－x+2；（2）6
【解析】试题分析：（1）由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标，再由点A、B的坐标利用待定系数法即可得出直线AB的解析式；
（2）求出点C的坐标，利用三角形的面积公式结合A、B点的横坐标即可得出结论.
试题解析：（1）∵点A 、B在反比例函数y=－
的图像上，
∴y=
=4 ，x=
=4，
∴A、B两点的坐标为A(－2，4)，B(4，－2)，
又 ∵A、B两点在一次函数y=kx+b 的图像上，
∴－2k+b=4且4k+b=－2，
解得：k=－1，b=2，
∴一次函数y=－x+2；
（2）直线y=－x+2与y轴的交点为C（0，2），
线段
将△ABC分成△AOC和△BOC两个三角形，
∴S△ABO=S△AOC+S△BOC=
×2×2÷2＋
×4×2=6．
名师点拨卷系列答案
英才计划期末调研系列答案
【题目】小明同学积极参加体育锻炼，天天坚持跑步，他每天以3000m为标准，超过的米数记作正数，不足的米数记作负数．下表是他一周跑步情况的记录（单位：m）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与标准的差/m | +420 | +460 | ﹣100 | ﹣210 | ﹣330 | +200 | +150 |
（1）他星期三跑了 m；
（2）他跑得最多的一天比最少的一天多跑了多少m；
（3）若他跑步的平均速度为240m/min，求这周他跑步的时间．
【题目】在对第一章“丰富的图形世界”复习前，老师让学生整理正方体截面的形状并探究多面体（由若干个多边形所围成的几何体）的棱数、面数、顶点数之间的数量关系，如图是小颖用平面截正方体后剩余的多面体，请解答下列问题：
（1）根据上图完成下表：
多面体 | V（顶点数） | F（面数） | E（棱数） |
（1） |
| 7 | 15 |
（3） | 6 |
| 9 |
（5） | 8 | 6 |
|
（2）猜想：一个多面体的V（顶点数），F（面数），E（棱数）之间的数量关系是 ；
（3）计算：已知一个多面体有20个面、30条棱，那么这个多面体有 个顶点．
