题目内容
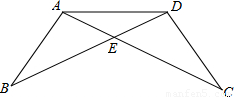
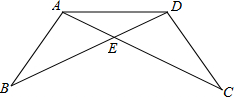在一次数学课上，陈老师在黑板上画出下图，并写下了四个等式：①AB=DC，②BE=CE，③∠B=∠C，④∠BAE=∠CDE．
要求同学从这四个等式中选出两个作为条件，推出△AED是等腰三角形．
（1）请你按陈老师的要求一一写出所有可能的条件
①③或①④或②③
①③或①④或②③
．（2）任选一种证明．
已知：
求证：△AED是等腰三角形．
证明：
分析：根据全等三角形的判定定理SAS进行解答即可．
解答：解：（1）①③或①④或②③；
（2）选②③证明，
∵∠AEB=∠DEC，BE=CE，∠B=∠C，
∴∠ABE≌∠DCE，
∴AE=DE，
∴AED为等腰三角形．
（2）选②③证明，
∵∠AEB=∠DEC，BE=CE，∠B=∠C，
∴∠ABE≌∠DCE，
∴AE=DE，
∴AED为等腰三角形．
点评：本题考查的是全等三角形的判定与性质、等腰三角形的判定，熟知以上知识是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
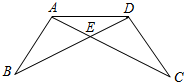在一次数学课上，王老师在黑板上画出图，如图，并写下了四个等式：①AB=DC，②BE=CE，③∠B=∠C，④∠BAE=∠CDE．要求同学从这四个等式中选出两个作为条件，推出△AED是等腰三角形．请你试着完成王老师提出的要求，并说明理由．（写出一种即可）
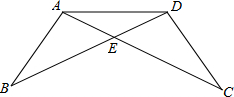在一次数学课上，陈老师在黑板上画出下图，并写下了四个等式：