题目内容
 如图,△ABC中,AB=3,BC=4,AC=5,E,F分别在AB,AC上,沿EF对折,使点A落在BC上的点D处,且FD⊥BC.
如图,△ABC中,AB=3,BC=4,AC=5,E,F分别在AB,AC上,沿EF对折,使点A落在BC上的点D处,且FD⊥BC.
(1)判断四边形AEDF的形状,并证明你的结论.
(2)求AD的长.
 (1)四边形AEDF是菱形.
(1)四边形AEDF是菱形.证明:因为AB=3,BC=4,AC=5,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,∠B=90°,
∴AB⊥BC,FD⊥BC,
∴AE∥FD,
∵由折叠的性质知,∠EAF=∠EDF,
∵FD⊥BC,
∴∠EDB+∠FDE=90°,
∵∠C+∠BAC=90°,
∴∠EDB=∠C,
∴ED∥AC,
∴四边形AEDF是平行四边形,
∵AF∥FD,
∴平行四边形AEDF是菱形.
(2)解:∵四边形AEDF是菱形,
∴ED=AE=FD=AF,
∵FD∥AB,
∴
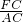 =
= ,
,∴
 =
= ,
,解得:DF=
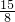 ,
,故BE=3-
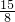 =
=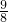 ,
,故BD=
 =
= =
=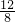 =
= ,
,则AD=
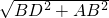 =
= .
.分析:(1)因为AC2=AB2+BC2,根据勾股定理和逆定理知,△ABC是直角三角形,∠B=90°,得出AB∥FD,由折叠的性质知,AF=DF,∠EAF=∠EDF,利用FD⊥BC得出∠EDB=∠C,则ED∥AC,得出四边形AEDF是平行四边形,再利用AF=FD,所以四边形AEDF是菱形.
(2)由(1)知,四边形AEDF是菱形,利用菱形的性质得出ED=AE=FD=AF,求出DE的长,再利用勾股定理求出BD的长,进而求得AD的值.
点评:本题考查了图形的翻折变换以及勾股定理和锐角三角函数关系等知识,利用折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等得出是解题关键.

练习册系列答案
相关题目
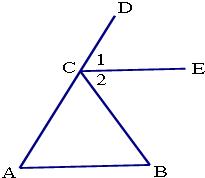 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.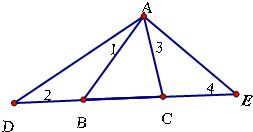 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )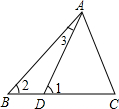 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.