��Ŀ����
����Ŀ��ij�ࡰ�����֡���ѧѧϰ����С��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��ʱ�������������⣬������һ���Խ��
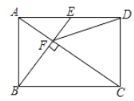
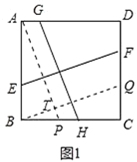
��1����ͼ1��������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����EF�� ��GH�����������=��������
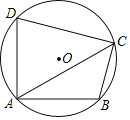
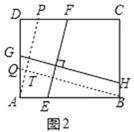
��2����ͼ2������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����֤��![]() =
=![]() ��
��
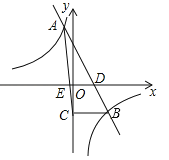
��3����ͼ3���ı���ABCD�У���ABC=��ADC=90�㣬BC=3��CD=5��AD=7��5��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��

���𰸡���1��=����2������������3��![]()
��������
��1�����ȹ���A��AP��GH����BC��P������B��BQ��EF����CD��Q����BQ��T��Ȼ����������ε������Լ���ABP�ա�BCQ���ж������ʣ����ɵó�EF=GH��
��2�����ȹ���A��AP��EF����CD��P������B��BQ��GH����AD��Q��Ȼ����ݾ��ε������Լ���PDA�ס�QAB���ж������ʣ����ɵó�![]() ��
��
��3�����ȹ���D��ƽ����AB��ֱ�ߣ�������Aƽ����BC��ֱ����R����BC���ӳ�����S���ж�ƽ���ı���ABSR�Ǿ��Σ��ɣ�1�����۵ó�![]() ��Ȼ���ж���ARD�ס�DSC�����������ʺ��ɶ����������̣���⼴��.
��Ȼ���ж���ARD�ס�DSC�����������ʺ��ɶ����������̣���⼴��.
��1����ͼ1�У�����A��AP��GH����BC��P������B��BQ��EF����CD��Q����BQ��T��
���ı���ABCD�������Σ�
��AB��DC��AD��BC��AB=BC����ABP=��C=90��
���ı���BEFQ���ı���PHGA����ƽ���ı��Σ�
��AP=GH��EF=BQ��
�֡�GH��EF��
��AP��BQ��
���PBT+��ABT=90�㣬��ABT+��BAT=90�㣬
���CBQ=��BAT��
�ڡ�ABP�͡�BCQ�У�
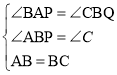 ��
��
���ABP�ա�BCQ��
��AP=BQ��
��EF=GH��
�ʴ�Ϊ��=��
��2������A��AP��EF����CD��P������B��BQ��GH����AD��Q����ͼ2��
���ı���ABCD�Ǿ��Σ�
��AB��DC��AD��BC��
���ı���AEFP���ı���BHGQ����ƽ���ı��Σ�
��AP=EF��GH=BQ��
�֡�GH��EF��
��AP��BQ��
���QAT+��AQT=90�㣬
���ı���ABCD�Ǿ��Σ�
���DAB=��D=90�㣬
���DAP+��DPA=90�㣬
���AQT=��DPA��
���PDA�ס�QAB��
��![]() ��
��
��![]()
![]() ��
��
��3������D��ƽ����AB��ֱ�ߣ�������Aƽ����BC��ֱ����R����BC���ӳ�����S����ͼ3��
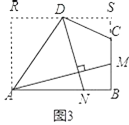
���ı���ABSR��ƽ���ı��Σ�
�ߡ�ABC=90�㣬
��ƽ���ı���ABSR�Ǿ��Σ�
���R=��S=90�㣬RS=AB=10��AR=BS��
��AM��DN��
���ɣ�1���еĽ��ۿɵ�![]() ��
��
��SC=x����AR=BS=3+x��
�ߡ�ADC=��R=��S=90�㣬
���ADR+��RAD=90�㣬��ADR+��SDC=90�㣬
���RAD=��CDS��
���ARD�ס�DSC��
��![]() =
=![]() =
=![]() ��
��
��DR=![]() x��DS=
x��DS=![]() ��x+3����
��x+3����
��Rt��ARD����AD2=AR2+DR2��
��7.52=��x+3��2+��![]() x��2��
x��2��
������13x2+24x��189=0�����x=3��![]() ��
��
��AR=6��AB=RS=![]() ��
��
��![]() =
=![]() .
.

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�