题目内容
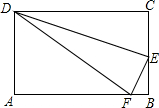 (2012•黑河)如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为
(2012•黑河)如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为| 289 |
| 8 |
| 289 |
| 8 |
分析:由AD=8,且△AFD的面积为60,即可求得AF与DF的长,由折叠的性质,可得CD=DF,然后在Rt△BEF中,利用勾股定理即可求得CE的长,继而求得△DEC的面积.
解答:解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,BC=AD=8,CD=AB,
∵△AFD的面积为60,
即
AD•AF=60,
解得:AF=15,
∴DF=
=17,
由折叠的性质,得:CD=DF=17,
∴AB=17,
∴BF=AB-AF=17-15=2,
设CE=x,则EF=CE=x,BE=BC-CE=8-x,
在Rt△BEF中,EF2=BF2+BE2,
即x2=22+(8-x)2,
解得:x=
,
即CE=
,
∴△DEC的面积为:
CD•CE=
×17×
=
.
故答案为:
.
∴∠A=∠B=90°,BC=AD=8,CD=AB,
∵△AFD的面积为60,
即
| 1 |
| 2 |
解得:AF=15,
∴DF=
| AD2+AF2 |
由折叠的性质,得:CD=DF=17,
∴AB=17,
∴BF=AB-AF=17-15=2,
设CE=x,则EF=CE=x,BE=BC-CE=8-x,
在Rt△BEF中,EF2=BF2+BE2,
即x2=22+(8-x)2,
解得:x=
| 17 |
| 4 |
即CE=
| 17 |
| 4 |
∴△DEC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 4 |
| 289 |
| 8 |
故答案为:
| 289 |
| 8 |
点评:此题考查了矩形的性质、折叠的性质、勾股定理以及三角形面积问题.此题难度适中,注意掌握数形结合思想与方程思想的应用,注意折叠中的对应关系.

练习册系列答案
相关题目
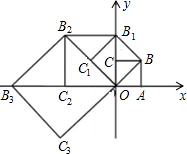 (2012•黑河)如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2012的坐标为
(2012•黑河)如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2012的坐标为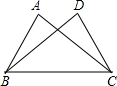 (2012•黑河)如图,已知AC=BD,要使△ABC≌△DCB,则只需添加一个适当的条件是
(2012•黑河)如图,已知AC=BD,要使△ABC≌△DCB,则只需添加一个适当的条件是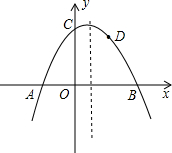 (2012•黑河)如图,抛物线y=-
(2012•黑河)如图,抛物线y=-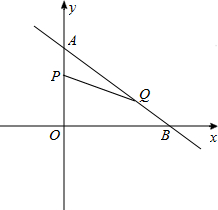 点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.