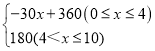题目内容
【题目】如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=____ _°.
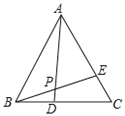
【答案】60
【解析】
试题分析:本题考查了等边三角形的性质,全等三角形的性质和判定,三角形外角性质的应用,解此题的关键是求出△ABD≌△BCE.根据等边三角形性质得出∠ABD=∠C=60°,AB=BC,证出△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,根据三角形外角性质得出∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC,即可得出答案.
解:∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC,
在△ABD和△BCE中,
AB=BC∠ABD=∠CBD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.
故选C.

练习册系列答案
相关题目
【题目】某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )
成绩(分) | 30 | 29 | 28 | 26 | 18 |
人数(人) | 32 | 4 | 2 | 1 | 1 |
A. 该班共有40名学生
B. 该班学生这次考试成绩的平均数为29.4分
C. 该班学生这次考试成绩的众数为30分
D. 该班学生这次考试成绩的中位数为28分