题目内容
【题目】(2016浙江省温州市第9题)如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
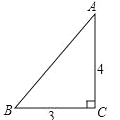
A.c>a>b B.b>a>c C.c>b>a D.b>c>a
【答案】D
【解析】
试题分析:(1)图1,根据折叠得:DE是线段AC的垂直平分线,由中位线定理的推论可知:DE是△ABC的中位线,得出DE的长,即a的长;(2)图2,同理可得:MN是△ABC的中位线,得出MN的长,即b的长;(3)图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.
第一次折叠如图1,折痕为DE, 由折叠得:AE=EC=![]() AC=
AC=![]() ×4=2,DE⊥AC ∵∠ACB=90° ∴DE∥BC
×4=2,DE⊥AC ∵∠ACB=90° ∴DE∥BC
∴a=DE=![]() BC=
BC=![]() ×3=
×3=![]()
第二次折叠如图2,折痕为MN, 由折叠得:BN=NC=![]() BC=
BC=![]() ×3=
×3=![]() ,MN⊥BC ∵∠ACB=90° ∴MN∥AC
,MN⊥BC ∵∠ACB=90° ∴MN∥AC
∴b=MN=![]() AC=
AC=![]() ×4=2
×4=2
第三次折叠如图3,折痕为GH,由勾股定理得:AB=![]() =5
=5
由折叠得:AG=BG=![]() AB=
AB=![]() ×5=
×5=![]() ,GH⊥AB ∴∠AGH=90° ∵∠A=∠A,∠AGH=∠ACB
,GH⊥AB ∴∠AGH=90° ∵∠A=∠A,∠AGH=∠ACB
∴△ACB∽△AGH ∴![]() =
=![]() ∴
∴![]() =
=![]() ∴GH=
∴GH=![]() ,即c=
,即c=![]() ∵2>
∵2>![]() >
>![]() ∴b>c>a
∴b>c>a




练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
