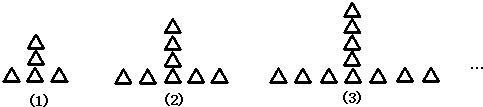题目内容
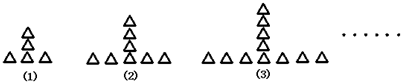
14、按如下规律摆放三角形,则第(5)堆三角形的个数为

67
.
分析:n=1时,三角形的个数为1+3×2=1+(2+1)×(1+1)
n=2时,三角形的个数为1+5×3=1+(2×2+1)×(2+1)
n=3时,三角形的个数为1+7×4=1+(2×3+1)×(3+1)
…
n=n时,三角形的个数为1+(2×n+1)×(n+1)
n=2时,三角形的个数为1+5×3=1+(2×2+1)×(2+1)
n=3时,三角形的个数为1+7×4=1+(2×3+1)×(3+1)
…
n=n时,三角形的个数为1+(2×n+1)×(n+1)
解答:解:由分析可知,当n=5时,三角形的个数为1+(2×5+1)×(5+1)=67.
点评:解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.

练习册系列答案
相关题目