题目内容
（2009•娄底）如图，AB是⊙O的弦，OD⊥AB于D交⊙O于E，则下列说法错误的是（ ）
A．AD=BD
B．∠ACB=∠AOE
C．
D．OD=DE
【答案】分析：由垂径定理和圆周角定理可证，AD=BD，AD=BD，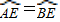
，而点D不一定是OE的中点，故D错误．
解答：解：∵OD⊥AB
∴由垂径定理知，点D是AB的中点，有AD=BD，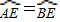
，
∴△AOB是等腰三角形，OD是∠AOB的平分线，
有∠AOE=
∠AOB，
由圆周角定理知，∠C=
∠AOB，
∴∠ACB=∠AOE，
故A、B、C正确，
D中点D不一定是OE的中点，故错误．
故选D．
点评：本题利用了垂径定理，等腰三角形的性质和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
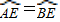，而点D不一定是OE的中点，故D错误．解答：解：∵OD⊥AB
∴由垂径定理知，点D是AB的中点，有AD=BD，
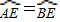，∴△AOB是等腰三角形，OD是∠AOB的平分线，
有∠AOE=
∠AOB，由圆周角定理知，∠C=
∠AOB，∴∠ACB=∠AOE，
故A、B、C正确，
D中点D不一定是OE的中点，故错误．
故选D．
点评：本题利用了垂径定理，等腰三角形的性质和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
阅读快车系列答案
相关题目
