题目内容
（2009•娄底）如图，已知AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于C，AB=3cm，PB=4cm，则BC= cm．
【答案】分析：根据切线的性质可知∠ABP=90°，又AB是⊙O的直径，可知∠ACB=90°，故根据勾股定理可将斜边AP求出；再根据三角形面积的求法，从而将斜边的高求出．
解答：解：∵PB是⊙O的切线，
∴∠ABP=90°，
∵AB=3cm，PB=4cm，
∴AP=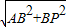
=
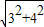=5；
∵AB是⊙O的直径，
∴∠ACB=90°，
即BC为△ABP的高；
∵
×AB×BP=
×AP×BC，
即
×3×4=
×5×BC，
∴BC=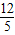
．
点评：本题综合考查了切线和圆周角的求法及性质．
解答：解：∵PB是⊙O的切线，
∴∠ABP=90°，
∵AB=3cm，PB=4cm，
∴AP=
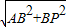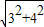==5；∵AB是⊙O的直径，
∴∠ACB=90°，
即BC为△ABP的高；
∵
×AB×BP=×AP×BC，即
×3×4=×5×BC，∴BC=
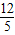．点评：本题综合考查了切线和圆周角的求法及性质．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
