题目内容
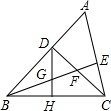 已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,F是CD边的中点,H是BC边的中点,连接DH与BE相交于点G,则下列结论正确的有
已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,F是CD边的中点,H是BC边的中点,连接DH与BE相交于点G,则下列结论正确的有
①BF=AC;②BF=2CE;③CE=BG;④DG=GH.
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:根据∠ABC=45°,CD⊥AB于D,可以证明△BCD是等腰直角三角形,然后根据等腰直角三角形的性质可得BD=CD,然后证明△BDF与△CDA全等,根据全等三角形对应边相等可得BF=AC,从而判断①正确;根据BE平分∠ABC,且BE⊥AC于E,可以证明△ABE与△CBE全等,根据全等三角形对应边相等可得AE=CE,从而判断②正确;过F作FM垂直BC交BC于M,可证BG:BF=1: =
= ,CE:BF=
,CE:BF= ,从而求解;过F作FM⊥BC,根据角平分线上的点到角的两边的距离相等可得DF=FM,所以DG=FM,从图中可以看出FM>GH,所以DG>GH,从而判断④错误.
,从而求解;过F作FM⊥BC,根据角平分线上的点到角的两边的距离相等可得DF=FM,所以DG=FM,从图中可以看出FM>GH,所以DG>GH,从而判断④错误.
解答:∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,
∴BD=CD,
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
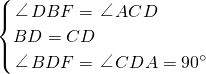 ,
,
∴△BDF≌△CDA(ASA),
∴BF=AC,故①正确;
∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,
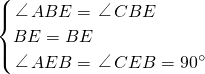 ,
,
∴△ABE≌△CBE(ASA),
∴AE=CE= AC,
AC,
∴BF=2CE,故②正确;
过F作FM垂直BC交BC于M,
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
∵F是CD的中点,FM⊥BC,
∴FM是△CDH的中位线,
∴FM垂直平分HC,
则BG:BF=1: =
= ,
,
CE:BF=
所以BG:CE=3,故③错误;

∵BE平分∠ABC,CD⊥AB于D,
∴FD=FM,
∴DG=FM,
从图可知,FM>GH,
∴DG>GH,故④错误.
综上所述,①②共2个正确.
故选B.
点评:本题考查了等腰直角三角形的判定与性质,角平分线的性质,全等三角形的判定与性质,仔细分析图形并熟练掌握各性质是解题的关键.
分析:根据∠ABC=45°,CD⊥AB于D,可以证明△BCD是等腰直角三角形,然后根据等腰直角三角形的性质可得BD=CD,然后证明△BDF与△CDA全等,根据全等三角形对应边相等可得BF=AC,从而判断①正确;根据BE平分∠ABC,且BE⊥AC于E,可以证明△ABE与△CBE全等,根据全等三角形对应边相等可得AE=CE,从而判断②正确;过F作FM垂直BC交BC于M,可证BG:BF=1:
 =
= ,CE:BF=
,CE:BF= ,从而求解;过F作FM⊥BC,根据角平分线上的点到角的两边的距离相等可得DF=FM,所以DG=FM,从图中可以看出FM>GH,所以DG>GH,从而判断④错误.
,从而求解;过F作FM⊥BC,根据角平分线上的点到角的两边的距离相等可得DF=FM,所以DG=FM,从图中可以看出FM>GH,所以DG>GH,从而判断④错误.解答:∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,
∴BD=CD,
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,

∴∠DBF=∠ACD,
在△BDF与△CDA中,
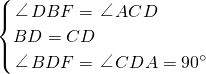 ,
,∴△BDF≌△CDA(ASA),
∴BF=AC,故①正确;
∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,
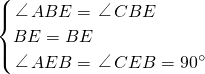 ,
,∴△ABE≌△CBE(ASA),
∴AE=CE=
 AC,
AC,∴BF=2CE,故②正确;
过F作FM垂直BC交BC于M,
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
∵F是CD的中点,FM⊥BC,
∴FM是△CDH的中位线,
∴FM垂直平分HC,
则BG:BF=1:
 =
= ,
,CE:BF=

所以BG:CE=3,故③错误;

∵BE平分∠ABC,CD⊥AB于D,
∴FD=FM,
∴DG=FM,
从图可知,FM>GH,
∴DG>GH,故④错误.
综上所述,①②共2个正确.
故选B.
点评:本题考查了等腰直角三角形的判定与性质,角平分线的性质,全等三角形的判定与性质,仔细分析图形并熟练掌握各性质是解题的关键.

练习册系列答案
相关题目
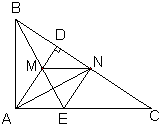 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.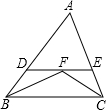 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.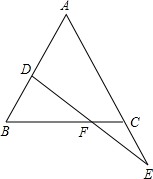 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.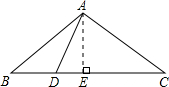 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.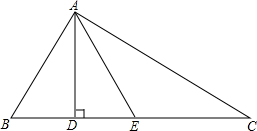 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.