题目内容
某人沿着坡度为1: 的山坡前进了1000 m,则这个人所在的位置升高了
的山坡前进了1000 m,则这个人所在的位置升高了
- A.1000m
- B.500m
- C.500
 m
m - D.
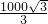 m
m
B
分析:根据坡度比可求出坡角,然后利用坡角的正弦值=垂直高度:坡面距离进行解答.
解答: 解:如图,AE=1000米.因为tanA=1:
解:如图,AE=1000米.因为tanA=1: ,
,
所以∠A=30°.
∴EF=AE•sinA=1000× =500米.
=500米.
故选B.
点评:此题主要考查学生对坡度与坡角的掌握及三角函数的运用.
分析:根据坡度比可求出坡角,然后利用坡角的正弦值=垂直高度:坡面距离进行解答.
解答:
 解:如图,AE=1000米.因为tanA=1:
解:如图,AE=1000米.因为tanA=1: ,
,所以∠A=30°.
∴EF=AE•sinA=1000×
 =500米.
=500米.故选B.
点评:此题主要考查学生对坡度与坡角的掌握及三角函数的运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
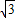 的山坡前进了1000 m,则这个人所在的位置升高了( )
的山坡前进了1000 m,则这个人所在的位置升高了( )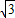 m
m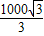 m
m 的山坡前进了100米,则此人所在的位置升高了( )
的山坡前进了100米,则此人所在的位置升高了( )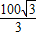
 的山坡前进了1000 m,则这个人所在的位置升高了( )
的山坡前进了1000 m,则这个人所在的位置升高了( )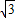 m
m m
m 的山坡前进了1000 m,则这个人所在的位置升高了( )
的山坡前进了1000 m,则这个人所在的位置升高了( ) m
m m
m 的山坡前进了1000米,则这个人所在的位置升高了 米.
的山坡前进了1000米,则这个人所在的位置升高了 米.