Question

【题目】正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直，

（1）证明：Rt△ABM ∽Rt△MCN；

（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；

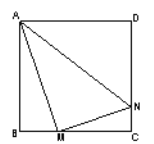（3）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值.

Answer 1

【答案】(1)、证明过程见解析；(2)、y=；最大值为10；(3)、BC的中点，x=2.

【解析】

试题分析：(1)、根据AM⊥MN得出∠CMN＋∠AMB= 90°，根据Rt△ABM得出∠CMN＝∠MAB，从而得出三角形相似；(2)、根据三角形相似得出CN与x的关系，然后根据梯形的面积计算法则得出函数解析式；(3)、根据要使三角形相似则需要满足，结合(1)中的条件得出BM=CM，即M为BC的中点.

试题解析：(1)在正方形ABCD中，AB＝BC＝CD＝4，∠B=∠C =90°，

∵AM⊥MN ∴∠AMN= 90°. ∴∠CMN＋∠AMB= 90°．

在Rt△ABM中，∠MAB＋∠AMB＝90°， ∴∠CMN＝∠MAB． ∴Rt△AMN∽Rt△MCN;

(2)∵Rt△ABM∽Rt△MCN， ∴ ∴ ∴CN=

∴y===

当x=2时，y取最大值，最大值为10；故当点肘运动到BC的中点时，四边形ABCN的面积最大，最大面积为10；

(3)∵∠B＝∠AMN= 90°， ∴要使Rt△ABM∽Rt△AMN，必须 有

由（1）知 ∴BM=MC

∴当点M运动到BC的中点时，Rt△ABM∽Rt△AMN，此时x=2