题目内容
如图,一块直角三角形木板ABC,其中∠C=90°,AC=3m,BC=4m,现在要把它们加工成一个面积最大的矩形,甲、乙两位木工师傅的加工方法分别如图1、图2所示,请用学过的知识说明哪位师傅的加工方法符合要求.

解:如图1,设DE=x,EF=y,矩形的面积记为S,
由题意,DE∥CB,
∴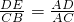
即: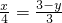
解得y=3- x其中0<x<4
x其中0<x<4
∴S=xy=x(3- x)=-
x)=- x2+3x=-
x2+3x=- (x-2)2+3
(x-2)2+3
∴有最大面积是3.
(2)如图,作CE⊥AB于点E,交 NM与点D
NM与点D
∵∠C=90°,AC=3m,BC=4m,
∴AB=5 CE=2.4
设MQ=x MN=y,则DE=x,CD=2.4-x
∵MN∥AB
∴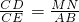
即:
整理得:y=- x+5
x+5
∴S=xy=x(- x+5)=-
x+5)=- (x-
(x- )2+3
)2+3
故两个师傅均符合要求.
分析:根据相似三角形求矩形的长与宽的函数关系式,然后表示出有关面积的函数关系式并求出其最大值,找到最大的方案即可.
点评:此题考查了相似三角形的性质,相似三角形的对应边成比例;解此题的关键是将实际问题转化为数学问题进行解答.
由题意,DE∥CB,
∴
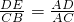
即:
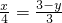
解得y=3-
 x其中0<x<4
x其中0<x<4∴S=xy=x(3-
 x)=-
x)=- x2+3x=-
x2+3x=- (x-2)2+3
(x-2)2+3∴有最大面积是3.
(2)如图,作CE⊥AB于点E,交
 NM与点D
NM与点D∵∠C=90°,AC=3m,BC=4m,
∴AB=5 CE=2.4
设MQ=x MN=y,则DE=x,CD=2.4-x
∵MN∥AB
∴
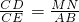
即:

整理得:y=-
 x+5
x+5∴S=xy=x(-
 x+5)=-
x+5)=- (x-
(x- )2+3
)2+3故两个师傅均符合要求.
分析:根据相似三角形求矩形的长与宽的函数关系式,然后表示出有关面积的函数关系式并求出其最大值,找到最大的方案即可.
点评:此题考查了相似三角形的性质,相似三角形的对应边成比例;解此题的关键是将实际问题转化为数学问题进行解答.

练习册系列答案
相关题目
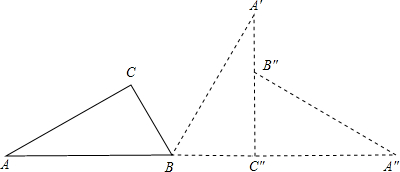

 如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积.
如图,一块直角三角形铁板被一块大铁板压在地面上,AB∥CD,已知CD=20,AB=30,BC=10,求直角三角形铁板被大铁板压住部分的面积. 如图有一块直角三角形纸片,∠A=30°,BC=
如图有一块直角三角形纸片,∠A=30°,BC= 如图在一块直角三角形地被分成BD分成两块,其中斜边AB长为13m,一条直角边BC长为
如图在一块直角三角形地被分成BD分成两块,其中斜边AB长为13m,一条直角边BC长为