题目内容
如图,直线y=-| 3 |
| 3 |
| 3 |
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求S与t之间的函数关系式.
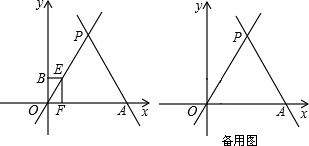
分析:(1)将两直线的解析式联立组成方程组,解得x、y的值即为两直线的交点坐标的横纵坐标;
(2)求得直线AP与x轴的交点坐标(4,0),利用OP=4PA=4得到OA=OP=PA从而判定△POA是等边三角形;
(3)分别求得OF和EF的值,利用三角形的面积计算方法表示出三角形的面积即可.
(2)求得直线AP与x轴的交点坐标(4,0),利用OP=4PA=4得到OA=OP=PA从而判定△POA是等边三角形;
(3)分别求得OF和EF的值,利用三角形的面积计算方法表示出三角形的面积即可.
解答: 解:(1)解方程组
解:(1)解方程组
,
解得:
.
∴点P的坐标为(2,2
);
(2)当y=0时,x=4,∴点A的坐标为(4,0).
∵OP=
=4PA=
=4,
∴OA=OP=PA,
∴△POA是等边三角形;
(3)
当0<t≤4时,S=
•OF•EF=
t2
当4<t<8时,S=-
t2+4
t-8
 解:(1)解方程组
解:(1)解方程组
|
解得:
|
∴点P的坐标为(2,2
| 3 |
(2)当y=0时,x=4,∴点A的坐标为(4,0).
∵OP=
22+(2
|
(2-4)2+(2
|
∴OA=OP=PA,
∴△POA是等边三角形;
(3)
当0<t≤4时,S=
| 1 |
| 2 |
| ||
| 8 |
当4<t<8时,S=-
3
| ||
| 8 |
| 3 |
| 3 |
点评:本题主要考查了一次函数的综合知识,解题的关键是正确的利用一次函数的性质求与坐标轴的交点坐标并转化为线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
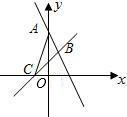 如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为
如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为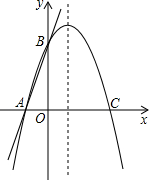 如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0). (2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
(2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).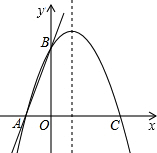 ,0).
,0).