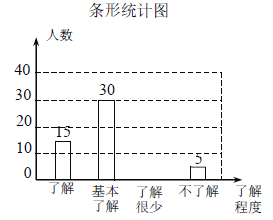
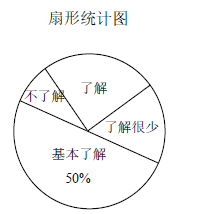
题目内容
【题目】如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.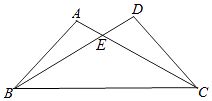
【答案】解:共5个:①或②或③或④或⑤.
若选①AE=DE,则证明如下:
在△ABE和△DCE中,
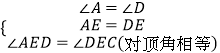 ,
,
∴AB=DC,BE=CE,
∴DE+BE=AE+CE,
∴BD=AC,
在△ABC和△DCB中,
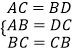 ,
,
∴△ABC≌△DCB(SSS);
若选②BE=CE,则证明如下:
证明:∵BE=CE
∴∠EBC=∠ECB,
在△ABC与△DCB中:
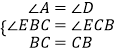 ,
,
∴△ABC≌△DCB(AAS);
若选③AB=DC,则证明如下:
在△ABE和△DCE中,
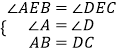 ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,
∴∠EBC=∠ECB,
在△ABC与△DCB中:
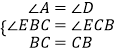 ,
,
∴△ABC≌△DCB(AAS);
若选④∠ABC=∠DCB,则证明如下:
证明:在△ABC与△DCB中:
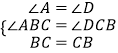 ,
,
∴△ABC≌△DCB(AAS);
若选⑤AC=BD,则证明如下:
如图,延长BA,CD交于点F,
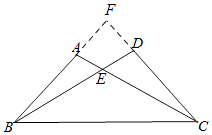
∵∠BAC=∠CDB,
∴∠FAC=∠FDB,
又∵∠F=∠F,BD=CA,
∴△BDF≌△CAF,
∴BF=CF,AF=DF,
∴AB=CD,
在△ABE和△DCE中,
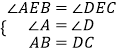 ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,
∴∠EBC=∠ECB,
在△ABC与△DCB中:
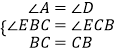 ,
,
∴△ABC≌△DCB(AAS).
综上所述,能证明△ABC与△DCB全等的条件有5个.
【解析】若已知两边对应相等,则找它们的夹角或第三边,若已知两角对应相等,则必须再找一组对边对应相等,若已知一边一角对应相等,则找令一组角,或找这个角得令一组对应邻边。

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目