题目内容
下列命题:
①若b=2a+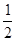 c,则一元二次方程a
c,则一元二次方程a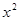 +bx+c=O必有一根为-2;
+bx+c=O必有一根为-2;
②若ac<0, 则方程 c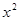 +bx+a=O有两个不等实数根;
+bx+a=O有两个不等实数根;
③若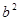 -4ac="0," 则方程 c
-4ac="0," 则方程 c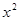 +bx+a=O有两个相等实数根;
+bx+a=O有两个相等实数根;
其中正确的个数是( )
①若b=2a+
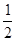 c,则一元二次方程a
c,则一元二次方程a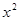 +bx+c=O必有一根为-2;
+bx+c=O必有一根为-2;②若ac<0, 则方程 c
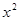 +bx+a=O有两个不等实数根;
+bx+a=O有两个不等实数根;③若
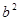 -4ac="0," 则方程 c
-4ac="0," 则方程 c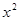 +bx+a=O有两个相等实数根;
+bx+a=O有两个相等实数根;其中正确的个数是( )
| A.O个 | B.l个 | C.2个 | D.3 个 |
C
分析:①将b=2a+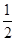 c代入方程,利用是自相乘法进行计算;
c代入方程,利用是自相乘法进行计算;
②利用ac<0和根的判别式进行判断即可;
③根据一元二次方程成立的条件解答.
解答:解:①将b=2a+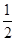 c代入方程得,2ax2+(4a+c)x+2c=0,
c代入方程得,2ax2+(4a+c)x+2c=0,
即(x+2)(2ax+c)=0,
解得x=-2或x=-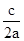 ,必有一根为-2.
,必有一根为-2.
②cx2+bx+a=O中,△=b2-4ac,
∵ac<0,
∴b2-4ac>0.
故方程cx2+bx+a=O有两个不等实数根.
③cx2+bx+a=O中,当c=0,b≠0时,方程为一元一次方程,不会有两个相等实数根.
①②正确,
故选C.
 c代入方程,利用是自相乘法进行计算;
c代入方程,利用是自相乘法进行计算;②利用ac<0和根的判别式进行判断即可;
③根据一元二次方程成立的条件解答.
解答:解:①将b=2a+
 c代入方程得,2ax2+(4a+c)x+2c=0,
c代入方程得,2ax2+(4a+c)x+2c=0,即(x+2)(2ax+c)=0,
解得x=-2或x=-
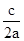 ,必有一根为-2.
,必有一根为-2.②cx2+bx+a=O中,△=b2-4ac,
∵ac<0,
∴b2-4ac>0.
故方程cx2+bx+a=O有两个不等实数根.
③cx2+bx+a=O中,当c=0,b≠0时,方程为一元一次方程,不会有两个相等实数根.
①②正确,
故选C.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
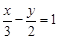 的一个解,则a= .
的一个解,则a= .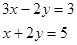 的解是( )
的解是( )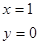



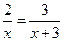
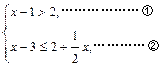
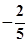 ____
____ ; 0____
; 0____ .
.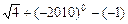 ;
; 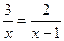 .
.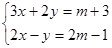 解的和为非正数,求m的取值范围.
解的和为非正数,求m的取值范围.