题目内容
如图，在△ACB中，点D是AB边上的一点，且∠ACB=∠CDA；点E在BC边上，且点E到AC、AB的距离相等，连接AE交CD于点F．试判断△CEF的形状；并证明你的结论．分析：根据角平分线上的点到两边的距离相等可知点E在∠CAB的角平分线上，再根据角平分线的性质可知∠CEF=∠CFE，即可得出CF=CE，即三角形为等腰三角形．
解答：解：△CEF是等腰三角形，理由如下：
证明：∵点E到AC、AB的距离相等，
∴点E在∠CAB的平分线上，
∴AE平分∠CAB，
∴∠CAE=∠BAE，
∵∠CEA=180°-∠CAE-∠ACB，∠DFA=180°-∠DAE-∠ADC．
∵∠ACB=∠CDA，
∴∠CEA=∠DFA，
∵∠DFA=∠CFE，
∴∠CEF=∠CFE，
∴CF=CE．
∴△CEF是等腰三角形．
证明：∵点E到AC、AB的距离相等，
∴点E在∠CAB的平分线上，
∴AE平分∠CAB，
∴∠CAE=∠BAE，
∵∠CEA=180°-∠CAE-∠ACB，∠DFA=180°-∠DAE-∠ADC．
∵∠ACB=∠CDA，
∴∠CEA=∠DFA，
∵∠DFA=∠CFE，
∴∠CEF=∠CFE，
∴CF=CE．
∴△CEF是等腰三角形．
点评：本题主要考查了等腰三角形的判定以及角平分线的性质，难度适中．
练习册系列答案
相关题目
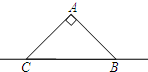（2012•虹口区二模）如图，在△ACB中，∠CAB=90°，AC=AB=3，将△ABC沿直线BC平移，顶点A、C、B平移后分别记为A1、C1、B1，若△ACB与△A1C1B1重合部分的面积2，则CB1=
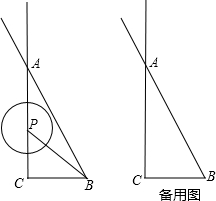（2012•邯郸二模）如图，在△ACB中，∠ACB=90°，AC=4，BC=2，点P为射线CA上的一个动点，以P为圆心，1为半径作⊙P．
如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（-2，0），点A的坐标为（-6，3），则B点的坐标是
如图：在△ACB中，点D是AB边上一点，且∠ACB=∠CDA，∠CAB的平分线分别交CD、BC于点E、F．